摘要:所以△AOC为等腰直角三角形.所以点C坐标为代入椭圆方程得.则椭圆方程为.(2)由直线CP.CQ与x轴围成底边在x轴上的等腰三角形.设直线CP的斜率为k.则直线CQ的斜率为-k.直线CP的方程为y-1=k(x-1).直线CQ的方程为y-1=-k(x-1).由椭圆方程与直线CP的方程联立.消去y得 (1+3k2)x2-6k(k-1)x+3k2-6k-1=0①因为C(1.1)在椭圆上.所以x=1是方程①的一个根.于是
网址:http://m.1010jiajiao.com/timu_id_528725[举报]
已知F1、F2是椭圆C:
+
=1(a>b>0)的左右焦点,点P是椭圆C上的动点.
(1)若椭圆C的离心率为
,且
•
的最大值为8,求椭圆C的方程;
(2)若△F1PF2为等腰直角三角形,求椭圆C的离心率.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(1)若椭圆C的离心率为
| ||
| 3 |
| PF1 |
| PF2 |
(2)若△F1PF2为等腰直角三角形,求椭圆C的离心率.
如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.

【解析】(Ⅰ)因为
又 是平面PAC内的两条相较直线,所以BD
是平面PAC内的两条相较直线,所以BD 平面PAC,
平面PAC,
而 平面PAC,所以
平面PAC,所以 .
.
(Ⅱ)设AC和BD相交于点O,连接PO,由(Ⅰ)知,BD 平面PAC,
平面PAC,
所以 是直线PD和平面PAC所成的角,从而
是直线PD和平面PAC所成的角,从而
 .
.
由BD 平面PAC,
平面PAC, 平面PAC,知
平面PAC,知 .在
.在 中,由
中,由
 ,得PD=2OD.因为四边形ABCD为等腰梯形,
,得PD=2OD.因为四边形ABCD为等腰梯形, ,所以
,所以 均为等腰直角三角形,从而梯形ABCD的高为
均为等腰直角三角形,从而梯形ABCD的高为 于是梯形ABCD面积
于是梯形ABCD面积
 在等腰三角形AOD中,
在等腰三角形AOD中,
所以
故四棱锥 的体积为
的体积为 .
.

【点评】本题考查空间直线垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明BD 平面PAC即可,第二问由(Ⅰ)知,BD
平面PAC即可,第二问由(Ⅰ)知,BD 平面PAC,所以
平面PAC,所以 是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由
是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由 算得体积
算得体积
查看习题详情和答案>>
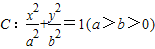 的左右焦点,点P是椭圆C上的动点.
的左右焦点,点P是椭圆C上的动点.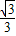 ,且
,且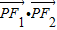 的最大值为8,求椭圆C的方程;
的最大值为8,求椭圆C的方程; 的左右焦点,点P是椭圆C上的动点.
的左右焦点,点P是椭圆C上的动点. ,且
,且 的最大值为8,求椭圆C的方程;
的最大值为8,求椭圆C的方程; 、
、 是椭圆
是椭圆 的左右焦点,点P是椭圆C上的动点.
的左右焦点,点P是椭圆C上的动点. ,且
,且 的最大值为8,求椭圆C的方程;
的最大值为8,求椭圆C的方程; P
P 为等腰直角三角形,求椭圆C的离心率.
为等腰直角三角形,求椭圆C的离心率.