0 49851 49859 49865 49869 49875 49877 49881 49887 49889 49895 49901 49905 49907 49911 49917 49919 49925 49929 49931 49935 49937 49941 49943 49945 49946 49947 49949 49950 49951 49953 49955 49959 49961 49965 49967 49971 49977 49979 49985 49989 49991 49995 50001 50007 50009 50015 50019 50021 50027 50031 50037 50045 447348
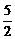 4
4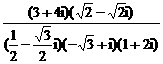 |-2i的模为_______________.
|-2i的模为_______________.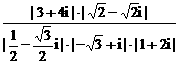 -2i
-2i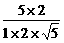 -2i=
-2i=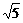 -2i,∴|z|=3.
-2i,∴|z|=3.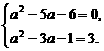 解得a=-1.
解得a=-1.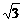 ,则
,则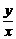 的最大值是
的最大值是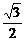 B.
B.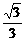 C.
C.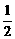 D.
D.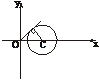
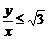 .
.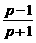 为纯虚数,则与复数p对应的点P
为纯虚数,则与复数p对应的点P 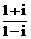 )n+(
)n+(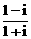 )n(n∈Z),则集合{x|x=f(n)}中元素的个数是
)n(n∈Z),则集合{x|x=f(n)}中元素的个数是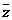 ∈R;
∈R;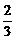 <m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
<m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于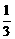 <m-1<0.
<m-1<0.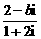 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于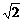 B.
B.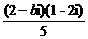 =
=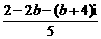
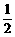 .
.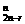 (
(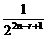 C
C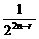 C
C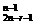 (
(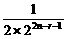 C
C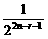 C
C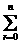
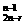 =1;
=1;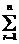
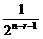 C
C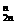
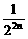 ,
,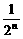 ;
;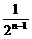 .
.