摘要:有点难度哟! 某数学家随身带着甲.乙两盒火柴.每盒有n根.每次用时.随机地任取一盒.然后从中抽取一根.求: (1)第一次发现一盒空时.另一盒恰剩r根火柴的概率(r=0.1.-.n), (2)第一次用完一盒火柴时另一盒恰剩r根火柴的概率(r=1.2.-.n). 分析:第n+1次取到甲盒时.才发现甲盒空.但第n次取甲盒后即已用完甲盒火柴.因此中的两个事件不同. 解:(1)记A=“首次发现一盒空时另一盒恰剩r根火柴 . B=“首次发现的空盒是甲盒且此时乙盒恰剩r根火柴 . C=“首次发现的空盒是乙盒且此时甲盒恰剩r根火柴 . 则事件B与C互斥.A=B+C. 由于甲.乙盒所处地位相同.故P(B)=P(C). 为求P(B).令D=“在甲.乙两盒中任取一盒.得到甲盒 .则P(D)=. 事件B发生相当于独立重复地做了2n-r+1次试验.前2n-r次D恰好发生n次.第2n-r+1次D也发生. 因此P(B)=C()n(1-)n-r· =C. P(A)=P(B)+P(C)=2P(B)=C. (2)记E=“首次用完一盒时另一盒恰有r根 . F(G)=“首次用完的是甲盒恰有r根火柴 . 则事件F与G互斥.E=F+G. 事件F发生相当于独立重复地做了2n-r次试验.前2n-r-1次D恰好发生n-1次.第2n-r次D也发生. 故P(F)=C()n-1(1-)n-r·=C. 类似(1).P(E)=P(F)+P(G)=2P(F)=C. 评述:改记A为Ar.则A0.A1.-.An彼此互斥.和是必然事件.故C=1, 改记E为Er.则E1.E2.-.En也彼此互斥.和是必然事件. 故C=1. 因此使用概率方法我们可以得到一些恒等式. (1)中分别取r=0和n.得 P(首次发现一盒空时另一盒也空)=C. P(首次发现一盒空时另一盒原封未动)=, (2)中取r=n.得 P(用完一盒时另一盒原封未动)=.
网址:http://m.1010jiajiao.com/timu3_id_499481[举报]
某数学家观察到:221+1=5;222+1=17;223+1=257;224+1=65537,于是该数学家猜想:任何形如22n+1 (n∈N*)都是质数,请判断该数学家的推理方式并对该结论给出正误判断( )
查看习题详情和答案>>
某市环保部门通过研究多年来该地区的大气污染状况后,建立了一个预测该市一天中的大气污染指标f(t)与时间t(单位:小时)之间的关系的函数模型:f(t)=|g(t)+
-a|+2a,t∈[0,24),其中,g(t)=
sin(
|t-18|)代表大气中某类随时间t变化的典型污染物质的含量;参数a代表某个已测定的环境气象指标,且a∈[0,
].
(1)求g(t)的值域;
(2)求f(t)的最大值M(a)的表达式;
(3)若该市政府要求每天的大气环境综合指数不得超过2.0,试问:若按给定的函数模型预测,该市目前的大气环境综合指数是否会超标?请说明理由. 查看习题详情和答案>>
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 24 |
| 3 |
| 4 |
(1)求g(t)的值域;
(2)求f(t)的最大值M(a)的表达式;
(3)若该市政府要求每天的大气环境综合指数不得超过2.0,试问:若按给定的函数模型预测,该市目前的大气环境综合指数是否会超标?请说明理由. 查看习题详情和答案>>
某数学家观察到:221+1=5;222+1=17;223+1=257;224+1=65537于是该数学家猜想:任何形如22n+1(n∈N*)都是质数,请判断该数学家的推理方式并对该结论给出正误判断( )
查看习题详情和答案>>
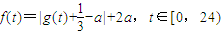 ,其中,
,其中,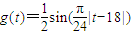 代表大气中某类随时间t变化的典型污染物质的含量;参数a代表某个已测定的环境气象指标,且
代表大气中某类随时间t变化的典型污染物质的含量;参数a代表某个已测定的环境气象指标,且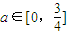 .
.