摘要: 已知:在△ABC中.以AC边为直径的⊙O交BC于点D.在劣弧 ⌒ AD上到一点E使∠EBC=∠DEC.延长BE依次交AC于G.交⊙O于H. (1)求证:AC⊥BH, (2)若∠ABC=45°.⊙O的直径等于10.BD=8.求CE的长. [答案]证明:⑴连接AD ∵∠DAC=∠DEC ∠EBC=∠DEC ∴∠DAC=∠EBC 又∵AC是⊙O的直径 ∴∠ADC=90° ∴∠DCA+∠DAC=90° ∴∠EBC+∠DCA=90° ∴∠BGC=180°-=180°-90°=90° ∴AC⊥BH ⑵∵∠BDA=180°-∠ADC=90°∠ABC=45° ∴∠BAD=45° ∴BD=AD ∵BD=8 ∴AD=8 又∵∠ADC=90° AC=10 ∴由勾股定理.得. ∴BC=BD+DC=8+6=14 又∵∠BGC=∠ADC=90° ∠BCG=∠ACD ∴△BCG∽△ACD ∴ ∴ ∴ 连接AE.∵AC是直径 ∴∠AEC=90° 又∵EG⊥AC ∴△CEG∽△CAE ∴ ∴ ∴.
网址:http://m.1010jiajiao.com/timu3_id_496146[举报]
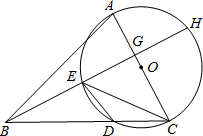 已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧 | AD |
(1)求证:AC丄BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长. 查看习题详情和答案>>
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH
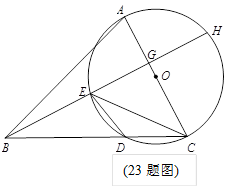 (2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
(2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
查看习题详情和答案>>
 (2012•鞍山二模)已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
(2012•鞍山二模)已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
 (2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
(2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.