摘要: 如图.以点O为圆心的两个同心圆中.矩形ABCD的边BC为大圆的弦.边AD与小圆相切于点M.OM的延长线与BC相交于点N. (1)点N是线段BC的中点吗?为什么? (2)若圆环的宽度为6cm.AB=5cm.BC=10cm.求小圆的半径. [答案]解:(1)N是BC的中点.原因:∵AD与小圆相切于点M. ∴OM⊥AD.又AD∥BC.∴ON⊥BC.∴在大圆O中.由垂径定理可得N是BC的中点. (2)连接OB.设小圆半径为r.则有ON=r+5,OB=r+6,BN=5cm, 在Rt△OBN中.由勾股定理得OB2=BN2+ON2 .即:(r+6)2=(r+5)2+52 .解得r=7cm. ∴小圆的半径为7cm.
网址:http://m.1010jiajiao.com/timu3_id_496144[举报]
 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,且AB=4,OP=2,连接OA交小圆于点E,则扇形OEP的面积为( )
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,且AB=4,OP=2,连接OA交小圆于点E,则扇形OEP的面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
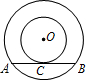 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点,若两圆的半径分别是10cm、6cm,则弦AB的长为( )
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点,若两圆的半径分别是10cm、6cm,则弦AB的长为( ) (1997•甘肃)如图,以点O为圆心的两个同心圆,大圆的弦AB交小圆于C、D,如果AB=3cm,CD=2cm,那么AC=
(1997•甘肃)如图,以点O为圆心的两个同心圆,大圆的弦AB交小圆于C、D,如果AB=3cm,CD=2cm,那么AC=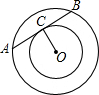 如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若AB=16,OC=6,则大圆的直径为
如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若AB=16,OC=6,则大圆的直径为 如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是
如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是