摘要： 如图.已知AB是⊙O的弦.OB=2.∠B=30°.C是弦AB上任意一点.连接CO并延长CO交⊙O于点D.连接AD. (1)弦长AB= , (2)当∠D=20°时.求∠BOD的度数, (3)当AC的长度为多少时.以点A.C.D为顶点的三角形与以B.C.O为顶点的三角形相似?请写出解答过程. [答案]解:(1)2. (2)解法一:∵∠BOD是△BOC的外角.∠BCO是△ACD的外角. ∴∠BOD=∠B+∠BCO.∠BCO=∠A+∠D. ∴∠BOD=∠B+∠A+∠D. 又∵∠BOD=2∠A.∠B=30°.∠D=20°. ∴2∠A=∠B+∠A+∠D=∠A+50°.∠A=50°. ∴∠BOD=2∠A=100°. 解法二:如图.连接OA. ∵OA=OB.OA=OD.∴∠BAO=∠B.∠DAO=∠D. ∴∠DAB=∠BAO+∠DAO=∠B+∠D. 又∵∠B=30°.∠D=20°.∴∠DAB=50°. ∴∠BOD=2∠DAB=100°. (3)∵∠BCO=∠A+∠D.∴∠BCO＞∠A.∠BCO＞∠D. ∴要使△DAC与△BOC相似.只能∠DCA=∠BCO=90°. 此时.∠BOC=60°.∠BOD=120°.∴∠DAC=60°. ∴△DAC∽△BOC. ∵∠BCO=90°.即OC⊥AB.∴AC=AB=.
网址：http://m.1010jiajiao.com/timu3_id_496142[举报]
如图，已知AB是⊙O的直径，P是AB延长线上一点，PC切⊙O于C，AD⊥PC于D，CE⊥AB于E，求证：
如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D=60°且AB=6，过O点作OE⊥AC，垂足为E．（1）求OE的长；
（2）若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积S．
如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．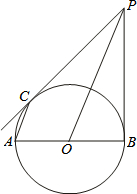
如图；已知AB是⊙O的直径，PB⊥AB，PC是⊙O的切线，切点为C．
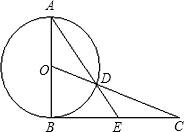如图，已知AB是⊙O的直径，BC是⊙O的切线，OC与⊙O相交于点D，连接AD并延长交BC于点E，BC=3，CD=2