摘要： 已知四边形ABCD是边长为4的正方形.以AB为直径在正方形内作半圆.P是半圆上的动点.连接PA.PB.PC.PD. (1)如图①.当PA的长度等于 时.∠PAB=60°, 当PA的长度等于 时.△PAD是等腰三角形, (2)如图②.以AB边所在的直线为x轴.AD边所在的直线为y轴.建立如图所示的直角坐标系.把△PAD.△PAB.△PBC的面积分别记为S1.S2.S3.设P点坐标为(a.b).试求2S1S3-S22的最大值.并求出此时a.b的值. [答案]解:(1)2,2或. (2)如图.过点P分别作PE⊥AB.PF⊥AD.垂足分别为E.F.延长FP交BC于点G.则PG⊥BC. ∵P点坐标为(a.b).∴PE=b.PF=a.PG=4-a. 在△PAD.△PAB及△PBC中. S1=2a.S2=2b.S3=8-2a. ∵AB是直径.∴∠APB=90°. ∴PE2=AE·BE.即b2=a(4-a). ∴2S1S3-S22=4a-4b2=-4a2+16a=-4(a-2)2+16. ∴当a=2时.b=2.2S1S3-S22有最大值16.
网址：http://m.1010jiajiao.com/timu3_id_496143[举报]
附加题：如图，已知四边形ABCD是边长为2的正方形，以对角线BD为边作正三角形BDE，过E作DA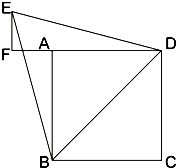
的延长线的垂线EF，垂足为F．
（1）找出图中与EF相等的线段，并证明你的结论；
（2）求AF的长． 查看习题详情和答案>>
的延长线的垂线EF，垂足为F．（1）找出图中与EF相等的线段，并证明你的结论；
（2）求AF的长． 查看习题详情和答案>>
已知四边形ABCD是边长为4的正方形，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PB、PC、PD．（1）当PA的长度为
2
2
时，∠PAB=60°；（2）当PA的长度为
2
或
| 2 |
8
| ||
| 5 |
2
或
时，△PAD是等腰三角形；| 2 |
8
| ||
| 5 |
（3）过点P作PE⊥PC交射线AB于E，延长BP交射线AD于F，试证明：AE=AF．
已知四边形ABCD是边长为4的正方形，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PB、PC、PD．
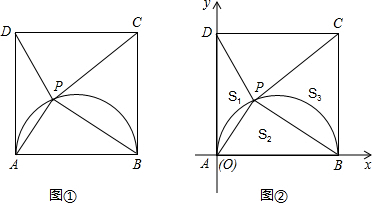
（1）如图①，当PA的长度等于 时，∠PAD=60°；当PA的长度等于 时，△PAD是等腰三角形；
（2）如图②，以AB边所在直线为x轴、AD边所在直线为y轴，建立如图所示的直角坐标系（点A即为原点O），把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3．设P点坐标为（a，b），试求2S1S3-S22的最大值，并求出此时a、b的值． 查看习题详情和答案>>
（1）如图①，当PA的长度等于
（2）如图②，以AB边所在直线为x轴、AD边所在直线为y轴，建立如图所示的直角坐标系（点A即为原点O），把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3．设P点坐标为（a，b），试求2S1S3-S22的最大值，并求出此时a、b的值． 查看习题详情和答案>>
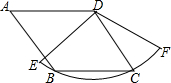（2013•浦东新区二模）如图，已知四边形ABCD是边长为2的菱形，点E、B、C、F都在以O为圆心的同一圆弧上，且∠ADE=∠CDF，那么
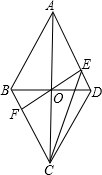（2013•株洲）已知四边形ABCD是边长为2的菱形，∠BAD=60°，对角线AC与BD交于点O，过点O的直线EF交AD于点E，交BC于点F．