摘要: 已知:如图.以矩形ABCD的对角线AC的中点O为圆心.OA长为半径作⊙0.⊙O经过B.D两点.过点B作BK⊥AC.垂足为K.过D作DH∥KB.DH分别与AC.AB.⊙O及CB的延长线相交于点E.F.G.H. (1)求证:AE=CK, (2)如果AB=.AD= (为大于零的常数).求BK的长, (3)若F是EG的中点.且DE=6.求⊙O的半径和GH的长. [答案] 解:(1)∵DH∥KB.BK⊥AC.∴DE⊥AC. ∵四边形ABCD是矩形.∴AD∥BC.AD=BC.∴∠EAD=∠KCB. ∴Rt△ADE≌Rt△CBK.∴AE=CK. (2)在Rt△ABC中.AB=.AD=BC=.∴==. ∵S△ABC=AB×BC=AC×BK.∴BK===. (3)连线OG.∵AC⊥DG.AC是⊙O的直接.DE=6.∴DE=EG=6.又∵EF=FG.∴EF=3,∵Rt△ADE≌Rt△CBK.∴DE=BK=6.AE=CK. 在△ABK中.EF=3.BK=6.EF∥BK.∴EF是△ABK的中位线.∴AF=BF.AE=EK=KC,在Rt△OEG中.设OG=.则OE=.EG=6..∴.∴. 在Rt△ADF≌Rt△BHF中.AF=BF. ∵AD=BC.BF∥CD.∴HF=DF. ∵FG=EF.∴HF-FG=DF-EF.∴HG=DE=6.
网址:http://m.1010jiajiao.com/timu3_id_496145[举报]
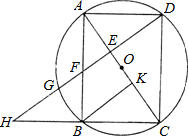 已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.(1)求证:AE=CK;
(2)如果AB=a,AD=
| 1 | 3 |
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长. 查看习题详情和答案>>
(2011•成都)已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
(1)求证:AE=CK;
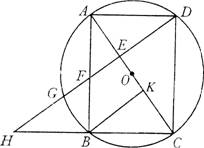
(2)如果AB=a,AD=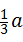 (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.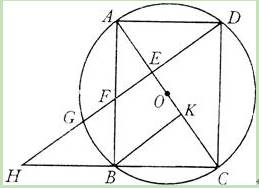
(本小题满分1 0分)
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥ A C,垂足为K。过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.

1.(1)求证:AE=CK;
2.(2)如果AB= ,AD=
,AD=![]() (
(![]() 为大于零的常数),求BK的长:
为大于零的常数),求BK的长:
3.(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
查看习题详情和答案>>
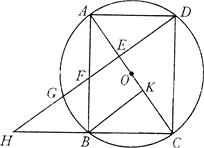
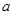 ,AD=
,AD=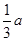 (
(
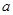 ,AD=
,AD=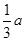 (
(