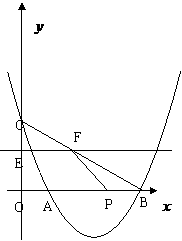
2、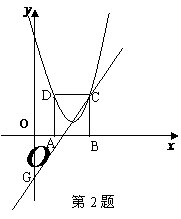 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=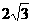 ,直线y=
,直线y=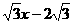 经过点C,交y轴于点G。
经过点C,交y轴于点G。
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=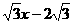 上且经过点C、D的抛物
上且经过点C、D的抛物
线的解析式;
(3)将(2)中的抛物线沿直线y=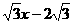 平移,平移后
平移,平移后
的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。
解:(1)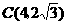
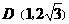
|
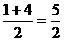 ,代入一次函数
,代入一次函数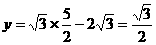 ,得顶点坐标为(
,得顶点坐标为(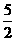 ,
,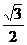 ),
),
∴设抛物线解析式为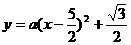 ,把点
,把点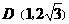 代入得,
代入得,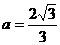
|
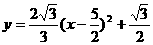
(3)设顶点E在直线上运动的横坐标为m,则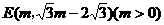
|
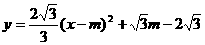
①当FG=EG时,FG=EG=2m,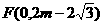 代入解析式得:
代入解析式得:
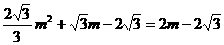 ,得m=0(舍去),
,得m=0(舍去),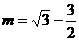 ,
,
|
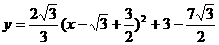 ;
;
②当GE=EF时,FG=4m,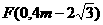 代入解析式得:
代入解析式得:
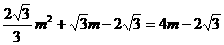 ,得m=0(舍去),
,得m=0(舍去),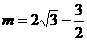 ,
,
|
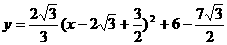 ;
;
③当FG=FE时,不存在;
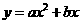 (a
(a 0)与反比例函数
0)与反比例函数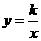 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点).
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点).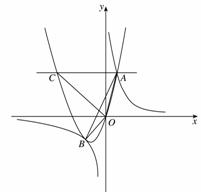
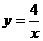 . ……………………………………… 1分
. ……………………………………… 1分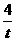 ),
),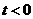 ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为 ,则有
,则有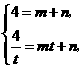 解得
解得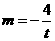 ,
,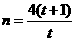 .
.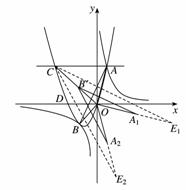 (3)直线AB与y轴的交点坐标为
(3)直线AB与y轴的交点坐标为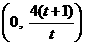 ,故
,故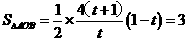 ,整理得
,整理得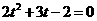 ,
,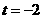 ,或t=
,或t=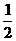 (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为( ,
,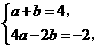 解得
解得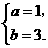
 点
点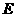 的坐标是(8,
的坐标是(8,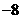 )……………… 2分
)……………… 2分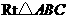 中,
中,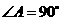 ,
,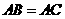 ,
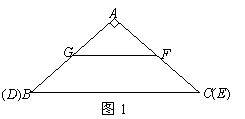
,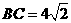 ,另有一等腰梯形
,另有一等腰梯形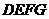 (
(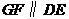 )的底边
)的底边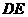 与
与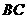 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点. ,将等腰梯形
,将等腰梯形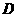 与点
与点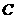 重合时停止.设运动时间为
重合时停止.设运动时间为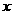 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为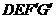 (如图2).
(如图2).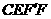 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时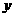 ,求
,求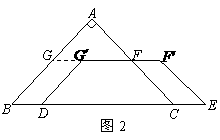
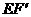 ,CE∥
,CE∥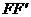 ,
, 四边形
四边形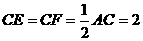 时,四边形
时,四边形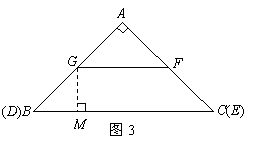 此时可求得
此时可求得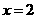 .
.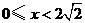 时,
时,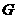 作
作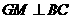 于
于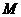 .
.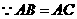 ,
,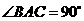 ,
,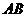 中点,
中点,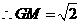 .
.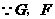 分别为
分别为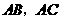 的中点,
的中点,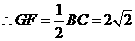 . ( 1分)
. ( 1分)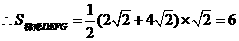
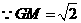 ,
,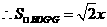 .
. 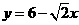 . ( 1分)
. ( 1分)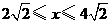 时,
时, 与
与 交于点
交于点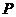 ,则
,则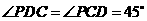 .
.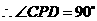 ,
,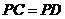 ,
,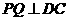 于
于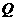 ,则.
,则. ( 1分)
( 1分)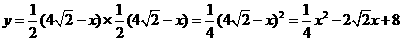 .
.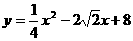 ( 1分)
( 1分)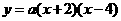 ,
, 代入得
代入得 .……………1分
.……………1分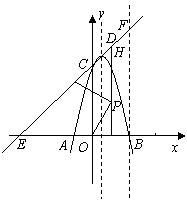
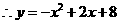
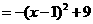 ,顶点
,顶点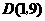 ……………2分
……………2分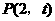 ,
,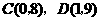 求得直线
求得直线 的解析式为
的解析式为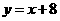 …………1分
…………1分 ,设
,设 的中垂线交
的中垂线交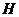 ,则
,则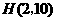 .
.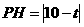 ,点
,点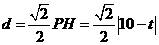 .
.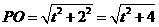 .
.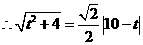 .
.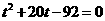 ,
,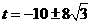 .……………1分
.……………1分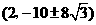 .……………1分
.……………1分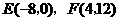 .
.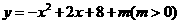 .
.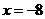 时,
时,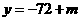 .
.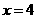 时,
时,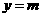 .
.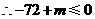 或
或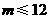 .……………1分
.……………1分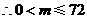 .
. 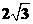 cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒. (2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.
(2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.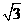
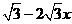 ……………2分
……………2分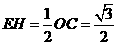 ∵DQ=x ∴BQ=2-x
∵DQ=x ∴BQ=2-x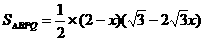 …………………………1分
…………………………1分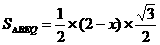 …………………………1分
…………………………1分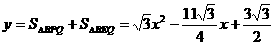 …………………………2分
…………………………2分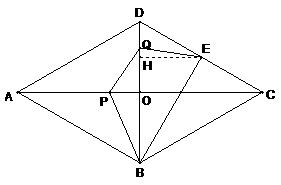 (2)能成为梯形,分三种情况:
(2)能成为梯形,分三种情况:
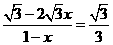 ∴x=
∴x=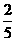
 ∴AP=
∴AP=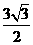 ,即
,即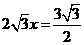
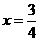
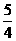 ≠PE,
≠PE,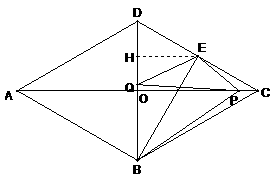 ∴x=
∴x=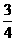 时,四边形PEQB为梯形.
…………………2分
时,四边形PEQB为梯形.
…………………2分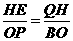 ∴
∴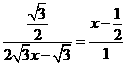
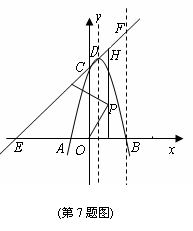 综上所述,当x=
综上所述,当x=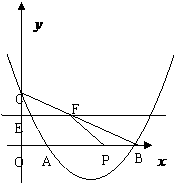 如图,抛物线
如图,抛物线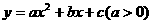 交
交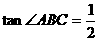 ,△ABC的面积为8.
,△ABC的面积为8.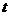 秒。当
秒。当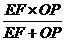 的值最大,并求出最大值;
的值最大,并求出最大值; 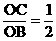
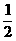 =4 ∴C(0,4)
=4 ∴C(0,4) 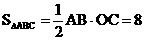 ∴AB = 4 A(4,0)
∴AB = 4 A(4,0) 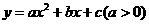 得
得 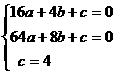 解得
解得 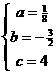
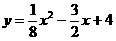 。
。
 (2)C ( 0, 4 ) B ( 8, 0
) E ( 0, 4-t ) ( t > 0)
(2)C ( 0, 4 ) B ( 8, 0
) E ( 0, 4-t ) ( t > 0)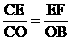 则有
则有 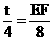 得 EF = 2t
得 EF = 2t 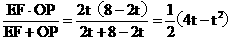 =
=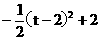
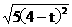
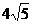
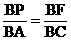 ,代入得
,代入得 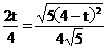 解得
解得 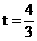

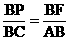 ,代入得
,代入得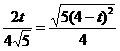 解得
解得 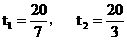 (不合题意,舍去)
(不合题意,舍去)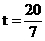 。
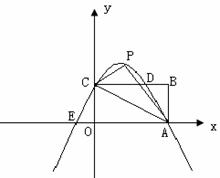
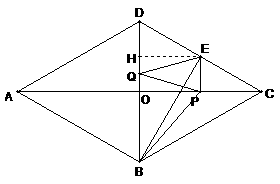
。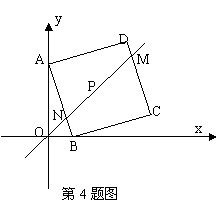 如图,P为正方形ABCD的对称中心,正方形ABCD的边长为
如图,P为正方形ABCD的对称中心,正方形ABCD的边长为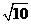 ,
,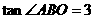 。直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以
。直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以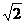 个单位每秒速度运动,运动时间为t。求:
个单位每秒速度运动,运动时间为t。求: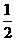 t2+2t(0<t≤4) ……… 1分
t2+2t(0<t≤4) ……… 1分 ……… 1分
……… 1分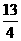 , S=
, S=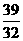 ……… 1分
……… 1分 , S=
, S=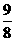 ……… 1分
……… 1分 , S=
, S= ……… 1分
……… 1分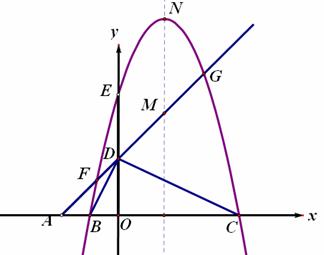
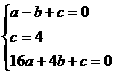 解得
解得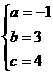 (2分)
∴
(2分)
∴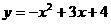 (1分)
(1分)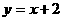 (1分)
(1分)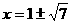 (
(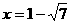 不符合,舍去)此时点P(
不符合,舍去)此时点P(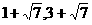 )
) 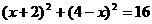 方程无解
方程无解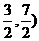 )N坐标是(
)N坐标是(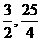 )∴MN=
)∴MN=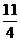
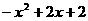
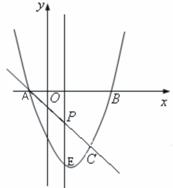
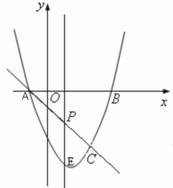 如图,抛物线
如图,抛物线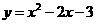 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线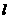 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.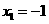 或
或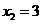
 将C点的横坐标x=2代入
将C点的横坐标x=2代入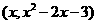
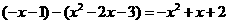 (2分)
(2分)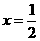 时,PE的最大值=
时,PE的最大值=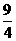 (1分)
(1分)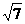 +4 ,0) F4(-
+4 ,0) F4(-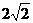 ,求EF的长;
,求EF的长;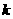 =PE∶CE,是否存在实数
=PE∶CE,是否存在实数