0 49339 49347 49353 49357 49363 49365 49369 49375 49377 49383 49389 49393 49395 49399 49405 49407 49413 49417 49419 49423 49425 49429 49431 49433 49434 49435 49437 49438 49439 49441 49443 49447 49449 49453 49455 49459 49465 49467 49473 49477 49479 49483 49489 49495 49497 49503 49507 49509 49515 49519 49525 49533 447348
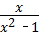 (
(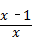 ﹣2),其中x=2.
﹣2),其中x=2.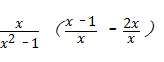 =
=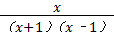 ×
×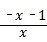 =
=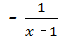 ,
,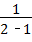 =﹣1.
=﹣1.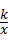 (k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足分别为B,C,如果△ABC的面积为3.则k的值为 6或﹣6 .
(k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足分别为B,C,如果△ABC的面积为3.则k的值为 6或﹣6 . |k|=3,
|k|=3,
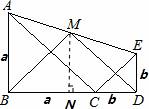
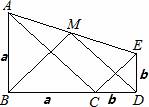
 ;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
 =
= =
=
 =5,
=5,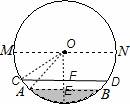
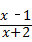 的值为零,则x的值是( )
的值为零,则x的值是( ) B、
B、
 D、
D、
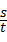 ,则v是t的反比例函数,且t>0.
,则v是t的反比例函数,且t>0.