摘要:过反比例函数y=图象上一点A.分别作x轴.y轴的垂线.垂足分别为B.C.如果△ABC的面积为3.则k的值为 6或﹣6 . 考点:反比例函数系数k的几何意义. 专题:计算题. 分析:根据△ABC的面积为反比例函数比例系数的绝对值的一半可得k的值. 解答:解:∵△ABC的面积为反比例函数比例系数的绝对值的一半. ∴|k|=3. 解得k=6或﹣6. 故答案为6或﹣6. 点评:考查反比例函数系数k的几何意义,得到△ABC的面积与反比例函数比例系数的关系是解决本题的关键.
网址:http://m.1010jiajiao.com/timu3_id_494369[举报]
 如图,过反比例函数y=
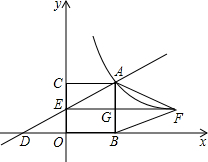
如图,过反比例函数y= 图象上一点A分别向x轴,y轴作垂线,垂足分别为点B,C,两条垂线与坐标轴所围成的图形为正方形,过点A的一次函数y=kx+1与x轴、y轴分别交于点D、E,作EF∥x轴,分别交AB和反比函数图象于点G、F,连接BF,AF.
图象上一点A分别向x轴,y轴作垂线,垂足分别为点B,C,两条垂线与坐标轴所围成的图形为正方形,过点A的一次函数y=kx+1与x轴、y轴分别交于点D、E,作EF∥x轴,分别交AB和反比函数图象于点G、F,连接BF,AF.
(1)求点A的坐标和一次函数解析式;
(2)求四边形ADBF的面积;
(3)猜想线段DE和线段BF有怎样的关系,并加以证明.
查看习题详情和答案>>
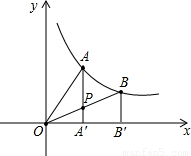
如图,过反比例函数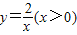 的图象上任意两点A,B分别作x轴的垂线,垂足为A',B',连接OA,OB,设AA'与OB的交点为P,△AOP与梯形PA'B'B的面积分别为S1,S2,比较它们的大小,可有( )
的图象上任意两点A,B分别作x轴的垂线,垂足为A',B',连接OA,OB,设AA'与OB的交点为P,△AOP与梯形PA'B'B的面积分别为S1,S2,比较它们的大小,可有( )
A.S1>S2
B.S1=S2
C.S1<S2
D.大小关系不能确定
查看习题详情和答案>>
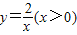 的图象上任意两点A,B分别作x轴的垂线,垂足为A',B',连接OA,OB,设AA'与OB的交点为P,△AOP与梯形PA'B'B的面积分别为S1,S2,比较它们的大小,可有( )
的图象上任意两点A,B分别作x轴的垂线,垂足为A',B',连接OA,OB,设AA'与OB的交点为P,△AOP与梯形PA'B'B的面积分别为S1,S2,比较它们的大小,可有( )
A.S1>S2
B.S1=S2
C.S1<S2
D.大小关系不能确定
查看习题详情和答案>>
 的图象上任意两点A,B分别作x轴的垂线,垂足为A',B',连接OA,OB,设AA'与OB的交点为P,△AOP与梯形PA'B'B的面积分别为S1,S2,比较它们的大小,可有( )
的图象上任意两点A,B分别作x轴的垂线,垂足为A',B',连接OA,OB,设AA'与OB的交点为P,△AOP与梯形PA'B'B的面积分别为S1,S2,比较它们的大小,可有( )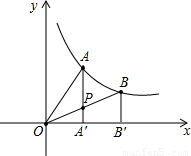
 的图象上一点分别作x、y轴的垂线段,如果垂线段与x、y轴所围成的矩形面积是5,则k=________.
的图象上一点分别作x、y轴的垂线段,如果垂线段与x、y轴所围成的矩形面积是5,则k=________.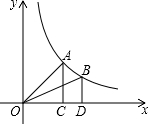 如图,过反比例函数
如图,过反比例函数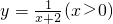 的图象上任意两点A、B分别作x轴的垂线,垂足分别不C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,比较它们的大小,可得
的图象上任意两点A、B分别作x轴的垂线,垂足分别不C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,比较它们的大小,可得