17.(本小题满分7分)
|
|
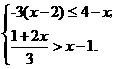
解不等式①,得 x 1
----------2分
1
----------2分
解不等式②,得 x<4.
所以,不等式组的解集为:
1 x<4 ---------------------------4分
x<4 ---------------------------4分
在数轴上表示为:
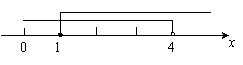
--------------------------6分
17.(本小题满分7分)
|
|
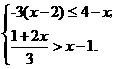
解不等式①,得 x 1
----------2分
1
----------2分
解不等式②,得 x<4.
所以,不等式组的解集为:
1 x<4 ---------------------------4分
x<4 ---------------------------4分
在数轴上表示为:

--------------------------6分