摘要：如图.PA.PB是⊙O是切线.A.B为切点.AC是⊙O的直径.若∠BAC=25°.则∠P= 50 度． 考点:切线的性质,多边形内角与外角. 专题:几何图形问题. 分析:首先利用切线长定理可得PA=PB.再根据∠OBA=∠BAC=25°.得出∠ABP的度数.再根据三角形内角和求出． 解答:解:∵PA.PB是⊙O是切线.A.B为切点. ∴PA=PB.∠OBP=90°. ∵OA=OB. ∴∠OBA=∠BAC=25°. ∴∠ABP=90°﹣25°=65°. ∵PA=PB. ∴∠BAP=∠ABP=65°. ∴∠P=180°﹣65°﹣65°=50°. 故答案为:50°． 点评:此题主要考查了切线的性质以及三角形内角和定理.得出∠ABP是解决问题的关键．
网址：http://m.1010jiajiao.com/timu3_id_494368[举报]
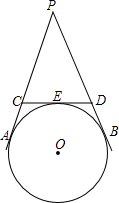如图，PA、PB、CD是⊙O的切线，A、B、E是切点，CD分别交线段PA、PB于C、D两点，若∠APB=40°，则∠COD的度数为（ ）| A、50° | B、60° | C、70° | D、75° |
如图，PA、PB、CD是⊙O的切线，A、B、E是切点，CD分别交PA、PB于C、D两点，若∠APB=40°，PA=5，则下列结论：①PA=PB=5；②△PCD的周长为5；③∠COD=70°．正确的个数为（ ）
查看习题详情和答案>>
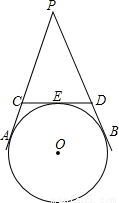如图，PA、PB、CD是⊙O的切线，A、B、E是切点，CD分别交线段PA、PB于C、D两点，若∠APB=40°，则∠COD的度数为（ ）A．50°
B．60°
C．70°
D．75°
查看习题详情和答案>>
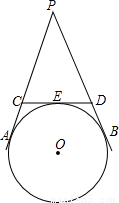如图，PA、PB、CD是⊙O的切线，A、B、E是切点，CD分别交线段PA、PB于C、D两点，若∠APB=40°，则∠COD的度数为（ ）
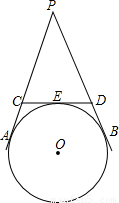如图，PA、PB、CD是⊙O的切线，A、B、E是切点，CD分别交线段PA、PB于C、D两点，若∠APB=40°，则∠COD的度数为（ ）