0 45669 45677 45683 45687 45693 45695 45699 45705 45707 45713 45719 45723 45725 45729 45735 45737 45743 45747 45749 45753 45755 45759 45761 45763 45764 45765 45767 45768 45769 45771 45773 45777 45779 45783 45785 45789 45795 45797 45803 45807 45809 45813 45819 45825 45827 45833 45837 45839 45845 45849 45855 45863 447348
 (1)过一点有且只有 条直线与已知直线垂直。
(1)过一点有且只有 条直线与已知直线垂直。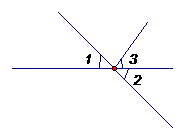 点到直线的距离:直线外一点到这条直线的
的长度。
点到直线的距离:直线外一点到这条直线的
的长度。 线段与角
线段与角 ,则
=
,则
=  ,则
=
,则
=  .
.
 .
. 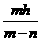 .
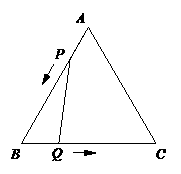
. 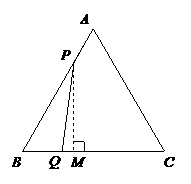 若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.
若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.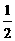 BP.
BP.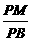 ,
,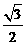 (3-t ).∴S△PBQ=
(3-t ).∴S△PBQ=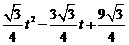 .
.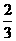 ,
,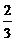 S△ABC .∴
S△ABC .∴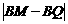 =
=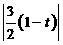 .
.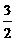 (1-t ) ]2+[
(1-t ) ]2+[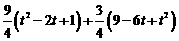 =
=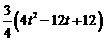 =3t2-9t+9.
=3t2-9t+9.
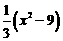 .∵y=
.∵y=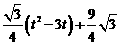 =
=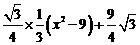 =
=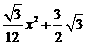 .
. 中,
中,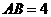 ,
,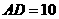 .直角尺的直角顶点
.直角尺的直角顶点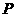 在
在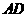 上滑动时(点
上滑动时(点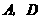 不重合),一直角边经过点
不重合),一直角边经过点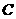 ,另一直角边
,另一直角边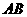 交于点
交于点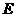 .我们知道,结论“
.我们知道,结论“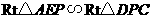 ”成立.
”成立.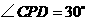 时,求
时,求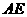 的长;
的长; (2)是否存在这样的点
(2)是否存在这样的点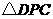 的周长等于
的周长等于 周长的
周长的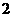 倍?若存在,求出
倍?若存在,求出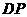 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.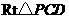 中,由
中,由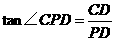 ,
,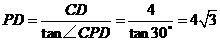
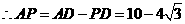 , 由
, 由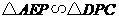 知
知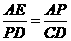 ,
,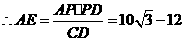 .
. 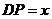 ,则
,则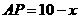
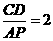 ,
,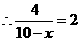 ,解得
,解得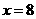 ,
, 此时
此时 ,
, 符合题意.
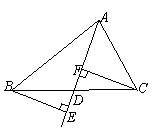
符合题意.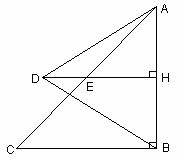 (2007重庆)已知,如图:△ABC是等腰直角三角形,∠ABC=900,AB=10,D为△ABC外一点,边结AD、BD,过D作DH⊥AB,垂足为H,交AC于E。
(2007重庆)已知,如图:△ABC是等腰直角三角形,∠ABC=900,AB=10,D为△ABC外一点,边结AD、BD,过D作DH⊥AB,垂足为H,交AC于E。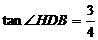 ,求DE的长。
,求DE的长。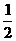 AB=5, ∴DH=
AB=5, ∴DH=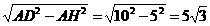
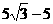
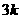 ,则DH=
,则DH=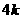 ,DB=
,DB=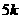
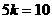 解得:
解得: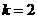
 (2007四川乐山)如图(11),在等边
(2007四川乐山)如图(11),在等边 中,点
中,点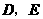 分别在边
分别在边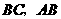 上,且
上,且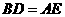 ,
, 交于点
交于点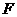 .
.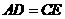 ;
;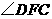 的度数.
的度数. 是等边三角形,
是等边三角形,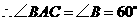 ,
,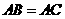
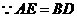
 ,················································································· 4分
,················································································· 4分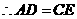 .······································································································· 5分
.······································································································· 5分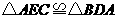 ,
,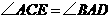 ······························································································· 6分
······························································································· 6分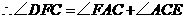
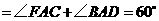 ······················································································ 9分
······················································································ 9分 如图,已知
如图,已知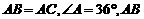 的中垂线
的中垂线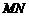 交
交 于点
于点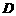 ,交
,交 于点
于点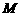 ,有下面4个结论:
,有下面4个结论: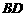 是
是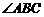 的角平分线;
的角平分线;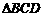 是等腰三角形;
是等腰三角形;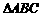 ∽
∽ ≌
≌