摘要:已知:如图.△ABC是边长3cm的等边三角形.动点P.Q同时从A.B两点出发.分别沿AB.BC方向匀速移 动.它们的速度都是1cm/s.当点P到达点B时.P.Q两 点停止运动.设点P的运动时间为t(s).解答下列问题: (1)当t为何值时.△PBQ是直角三角形? (2)设四边形APQC的面积为y(cm2).求y与t的 关系式,是否存在某一时刻t.使四边形APQC的面积是△ABC面积的三分之二?如果存在.求出相应的t值,不存在.说明理由, .试确定y与x之间的关系式. 解:⑴ 根据题意:AP=t cm.BQ=t cm. △ABC中.AB=BC=3cm.∠B=60°. ∴BP= cm. △PBQ中.BP=3-t.BQ=t. 若△PBQ是直角三角形.则∠BQP=90°或∠BPQ=90°. 当∠BQP=90°时.BQ=BP. 即t=. 当∠BPQ=90°时.BP=BQ.3-t=t.t=2 (秒). 答:当t=1秒或t=2秒时.△PBQ是直角三角形. ⑵ 过P作PM⊥BC于M .Rt△BPM中.sin∠B=. ∴PM=PB·sin∠B=.∴S△PBQ=BQ·PM=· t ·. ∴y=S△ABC-S△PBQ=×32×-· t ·=. ∴y与t的关系式为: y=. 假设存在某一时刻t.使得四边形APQC的面积是△ABC面积的. 则S四边形APQC=S△ABC .∴=××32×. ∴t 2-3 t+3=0.∵(-3) 2-4×1×3<0.∴方程无解. ∴无论t取何值.四边形APQC的面积都不可能是△ABC面积的.--8′ ⑶ 在Rt△PQM中.MQ==. MQ 2+PM 2=PQ 2.∴x2=[ ]2+[ ]2 ===3t2-9t+9. ∴t2-3t=.∵y=. ∴y===. ∴y与x的关系式为:y=.
网址:http://m.1010jiajiao.com/timu3_id_457666[举报]
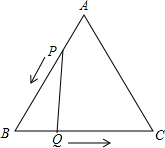 已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止当t=
已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止当t=1或2
1或2
时,△PBQ是直角三角形. 已知:如图,△ABC是边长为3cm等边三角形,动点P、Q分别同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P速度为1cm/s,点Q的速度为2cm/s,当点Q到达点C时,P、Q两点停止运动,设点P的运动时间为t(s),
已知:如图,△ABC是边长为3cm等边三角形,动点P、Q分别同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P速度为1cm/s,点Q的速度为2cm/s,当点Q到达点C时,P、Q两点停止运动,设点P的运动时间为t(s),(1)当t为何值时,△PBQ是直角三角形?
(2)△PBQ能否成为等边三角形?若能,请求出t值;若不存在,请说明理由.
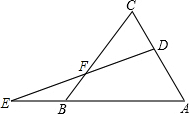 已知:如图,△ABC是边长为20cm的等边三角形,D为AC边上的一个动点,延长AB至E,使BE=CD,连接DE交BC于F.
已知:如图,△ABC是边长为20cm的等边三角形,D为AC边上的一个动点,延长AB至E,使BE=CD,连接DE交BC于F.(1)求证:DF=EF;
(2)如果D是AC的中点,求BF的长.
 时间为t(s),设四边形APQC的面积为y(cm2)
时间为t(s),设四边形APQC的面积为y(cm2)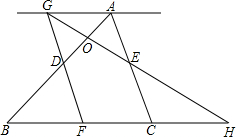 GE交AD于点O,并延长交BC延长线于点H.
GE交AD于点O,并延长交BC延长线于点H.