25. 王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
|
向上点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
出现次数 |
6 |
9 |
5 |
8 |
16 |
10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
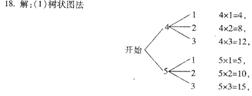
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
(1)出现向上点数为3的频率为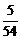 ,出现向上点数为5的频率为
,出现向上点数为5的频率为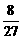
(2)都错
(3)画树状图或列表或简单说理(正确),概率P=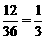 .
.
20.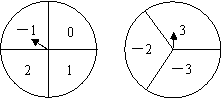 (1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,小颖胜.你认为这个游戏对双方公平吗? .(直接写出结果)
(1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,小颖胜.你认为这个游戏对双方公平吗? .(直接写出结果)
不公平,因为共有12个积,而其中的非负数有7个,
故P(小彬胜)=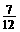 ,P(小颖胜)=
,P(小颖胜)=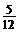 ,
,
P(小彬胜)>P(小颖胜),所以不公平.
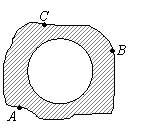 (2)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
(2)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
 |
50次 |
150次 |
300次 |
|
石子落在⊙O内(含⊙O上)的次数m |
14 |
43 |
93 |
|
石子落在阴影内的次数n |
19 |
85 |
186 |
你能否求出封闭图形ABC的面积?试试看.
由表可知,P(石子落在⊙O内)=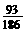 =0.5,故可估计S⊙O: S封闭图形ABC=0.5,因为S⊙O=
=0.5,故可估计S⊙O: S封闭图形ABC=0.5,因为S⊙O=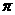 ,
,
所以S封闭图形ABC=2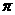 (m2).
(m2).
17.甲、乙两队进行拔河比赛,裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是:石头胜剪子,剪子胜布,布胜石头,手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平,为什么?(用树状图或列表法解答)
解:裁判员的这种作法对甲、乙双方是公平的.
理由:方法一:用列表法得出所有可能的结果如下:
|
甲 |
乙 |
||
|
石头 |
剪子 |
布 |
|
|
石头 |
(石头,石头) |
(石头,剪子) |
(石头,布) |
|
剪子 |
(剪子,石头) 21. |
(剪子,剪子) |
(剪子,布) |
|
布 |
(布,石头) |
(布,剪子) |
(布,布) |
根据表格得,P(甲获胜)=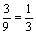 ,P(乙获胜)=
,P(乙获胜)=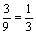
∵P(甲获胜)=P(乙获胜),
∴裁判员这种作法对甲、乙双方是公平的.
方法二:用树状图得出所有可能的结果如下:
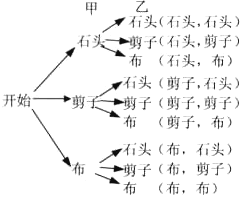
根据树状图,P(甲获胜)=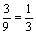 ,P(乙获胜)=
,P(乙获胜)=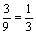 .
.
∵P(甲获胜)=P(乙获胜),
∴裁判员这种作法对甲、乙双方是公平的.
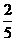 .
.
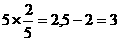 答:袋中有2个红球,3个白球. (2)
答:袋中有2个红球,3个白球. (2)
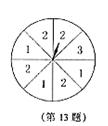 晓明玩转盘游戏,当他转动如图所示的转盘,转盘停止时指针指向2的概率是_________.
晓明玩转盘游戏,当他转动如图所示的转盘,转盘停止时指针指向2的概率是_________.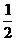 (或0.5,50%)
(或0.5,50%)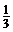
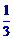
 甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜。清你解决下列问题:
甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜。清你解决下列问题: