摘要：已知.如图:△ABC是等腰直角三角形.∠ABC＝900.AB＝10.D为△ABC外一点.边结AD.BD.过D作DH⊥AB.垂足为H.交AC于E. (1)若△ABD是等边三角形.求DE的长, (2)若BD＝AB.且.求DE的长. 解:(1)∵△ABD是等边三角形.AB＝10.∴∠ADB＝600.AD＝AB＝10 ∵DH⊥AB ∴AH＝AB＝5. ∴DH＝ ∵△ABC是等腰直角三角形 ∴∠CAB＝450 ∴∠AEH＝450 ∴EH＝AH＝5.∴DE＝DH-EH＝ (2)∵DH⊥AB且. ∴可设BH＝.则DH＝.DB＝ ∵BD＝AB＝10 ∴ 解得: ∴DH＝8.BH＝6.AH＝4 又∵EH＝AH＝4. ∴DE＝DH-EH＝4
网址：http://m.1010jiajiao.com/timu3_id_457664[举报]
（2013•闵行区三模）已知：如图，△ABC是等边三角形，点D在边BC上，且△ADE是等边三角形．过点E作EF∥BC，EF分别与线段AB、AC、AD相交于点F、G、H，联结CE．（1）求证：四边形BCEF是平行四边形；
（2）如果AD⊥BC，求证：BC=2FG．
22、已知：如图，△ABC是等边三角形，D、E分别是BA、CA的延长线上的点，且AD=AE，连接ED并延长到F，使得EF=EC，连接AF、CF、BE．（1）求证：四边形BCFD是平行四边形；
（2）试指出图中与AF相等的线段，并说明理由．
24、已知：如图①，△ABC是等边三角形，四边形BDEF是菱形，其中DF=DB，连接AF、CD．
（1）观察图形，猜想AF与CD之间有怎样的数量关系？直接写出结论，不必证明；
（2）将菱形BDEF绕点B 按顺时针方向旋转，使菱形BDEF的一边落在等边△ABC内部，在图②中画出一个变换后的图形，并对照已知图形标记字母，请问：（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；
（3）在上述旋转过程中，AF、CD所夹锐角的度数是否发生变化？若不变，请你求出它的度数，并说明你的理由；若改变，请说明它的度数是如何变化的．
查看习题详情和答案>>
（1）观察图形，猜想AF与CD之间有怎样的数量关系？直接写出结论，不必证明；
（2）将菱形BDEF绕点B 按顺时针方向旋转，使菱形BDEF的一边落在等边△ABC内部，在图②中画出一个变换后的图形，并对照已知图形标记字母，请问：（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；
（3）在上述旋转过程中，AF、CD所夹锐角的度数是否发生变化？若不变，请你求出它的度数，并说明你的理由；若改变，请说明它的度数是如何变化的．
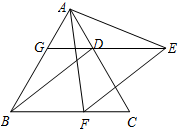18、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．
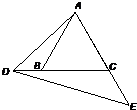24、已知，如图，△ABC是等边三角形，点D、E分别在CB、AC的延长线上，∠ADE=60°．