18、(2007浙江金华)水果种植大户小方,为了吸引更多的顾客,组织了观光采摘游活动.每一位来采摘水果的顾客都有一次抽奖机会:在一只不透明的盒子里有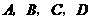 四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
(1)请利用树状图(或列表)的方法,表示前后两次抽得的卡片所有可能的情况;
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?

解:(1)方法一:列表得
|
|
A |
B |
C |
D |
 A A |
|
(A,B) |
(A,C) |
(A,D) |
|
B |
(B,A) |
|
(B,C) |
(B,D) |
|
C |
(C,A) |
(C,B) |
|
(C,D) |
|
D |
(D,A) |
(D,B) |
(D,C) |
|
方法二:画树状图
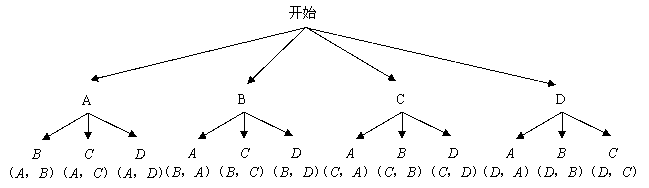

(2)获奖励的概率: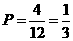 .
.
16、(2007四川成都)小华与小丽设计了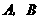 两种游戏:
两种游戏:
游戏 的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
游戏 的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
解:对游戏A:
画树状图
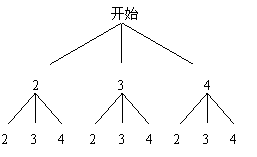
或用列表法
 |
2 |
3 |
4 |
|
2 |
 |
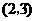 |
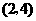 |
|
3 |
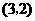 |
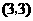 |
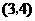 |
|
4 |
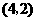 |
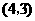 |
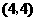 |
所有可能出现的结果共有9种,其中两数字之和为偶数的有5种,所以游戏 小华获胜的概率为
小华获胜的概率为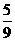 ,而小丽获胜的概率为
,而小丽获胜的概率为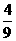 .即游戏
.即游戏 对小华有利,获胜的可能性大于小丽.
对小华有利,获胜的可能性大于小丽.
对游戏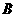 :
:
画树状图

或用列表法
 |
5 |
6 |
8 |
8 |
|
5 |
 |
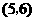 |
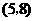 |
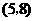 |
|
6 |
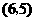 |
 |
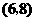 |
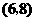 |
|
8 |
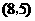 |
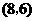 |
 |
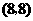 |
|
8 |
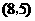 |
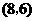 |
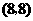 |
 |
所有可能出现的结果共有12种,其中小华抽出的牌面上的数字比小丽大的有5种;根据游戏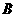 的规则,当小丽抽出的牌面上的数字与小华抽到的数字相同或比小华抽到的数字小时,则小丽获胜.所以游戏
的规则,当小丽抽出的牌面上的数字与小华抽到的数字相同或比小华抽到的数字小时,则小丽获胜.所以游戏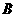 小华获胜的概率为
小华获胜的概率为 ,而小丽获胜的概率为
,而小丽获胜的概率为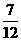 .即游戏
.即游戏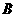 对小丽有利,获胜的可能性大于小华.
对小丽有利,获胜的可能性大于小华.
14、(2007潜江江汉油田)亲爱的同学,下面我们来做一个猜颜色的游戏:一个不透明的小盒中,装有A、B、C三张除颜色以外完全相同的卡片,卡片A两面均为红,卡片B两面均为绿,卡片C一面为红,一面为绿.
(1)从小盒中任意抽出一张卡片放到桌面上,朝上一面恰好是绿色,请你猜猜,抽出哪张卡片的概率为0?
(2)若要你猜(1)中抽出的卡片朝下一面是什么颜色,猜哪种颜色正确率可能高一些?请你列出表格,用概率的知识予以说明.
解:(1)依题意可知:抽出卡片 的概率为0;…………………(3分)
的概率为0;…………………(3分)
|
朝上 |
B(绿 1) |
B(绿 2) |
C(绿 ) |
|
朝下 |
B(绿 2) |
B(绿 1) |
C(红 ) |
(2)由(1)知,一定不会抽出卡片 ,只会抽出卡片
,只会抽出卡片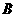 或
或 ,且抽出的卡片朝上的一面是绿色,那么可列下表:
,且抽出的卡片朝上的一面是绿色,那么可列下表:
………………………………(6分)
可见朝下一面的颜色有绿、绿、红三种可能,即:P(绿)=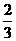 ,P(红)=
,P(红)=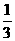 ,
,
所以猜绿色正确率可能高一些.
13、(2007贵州贵阳)小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
|
朝上的点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
出现的次数 |
7 |
9 |
6 |
8 |
20 |
10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.(4分)
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?(4分)
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.(4分)
解:(1)“3点朝上”出现的频率是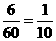 ······························································ 2分
······························································ 2分
“5点朝上”出现的频率是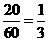 ················································································ 4分
················································································ 4分
(2)小颖的说法是错误的.这是因为,“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的频率最大.只有当实验的次数足够大时,该事件发生的频率稳定在事件发生的概率附近.························· 2分
小红的判断是错误的,因为事件发生具有随机性,故“6点朝上”的次数不一定是100次.
·················································································································· 4分
(3)列表如下:
 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
············································································· 2分
 ·················································································· 4分
·················································································· 4分
12、(2007广东韶关)不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),篮球1个。若从中任意摸出一个球,它是篮球的概率为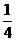 .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
解:(1)袋中黄球的个数为1个;····························2分
(2)方法一、列表如下:····························6分
|
* |
红1 |
红2 |
黄 |
蓝 |
|
红1 |
* |
(红1,红2) |
(红1,黄) |
(红1,蓝) |
|
红2 |
(红2,红1) |
* |
(红2,黄) |
(红2,蓝) |
|
黄 |
(黄,红1) |
(黄,红2) |
* |
(黄,蓝) |
|
蓝 |
(蓝,红1) |
(蓝,红2) |
(蓝,黄) |
* |
所以两次摸到不同颜色球的概率为: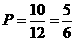 . ··························8分
. ··························8分
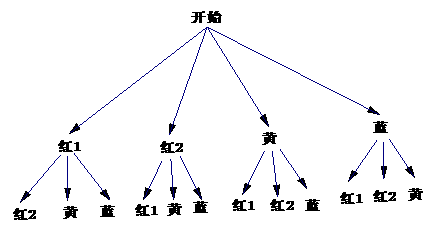 方法二,画树状图如下:
方法二,画树状图如下:




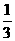 (B)
(B)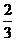 (C)
(C)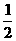 (D)
(D)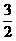
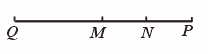
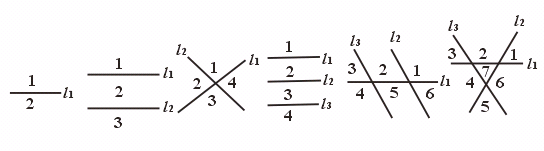

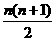 =
=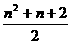 个部分,此时每两条直线都相交,且没有三条直线交于一点.
个部分,此时每两条直线都相交,且没有三条直线交于一点.

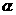 、
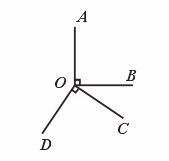
、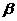 都是钝角,甲、乙、丙、丁四人计算
都是钝角,甲、乙、丙、丁四人计算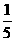
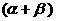 的结果依次是30°、
的结果依次是30°、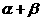 <360°.
<360°.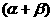 <72°.
<72°.
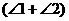 (B)
(B)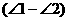 (D)
(D)


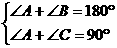 ,此时不能确定
,此时不能确定
 (2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。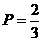
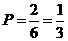 .
.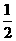 ;······································································································· 4分
;······································································································· 4分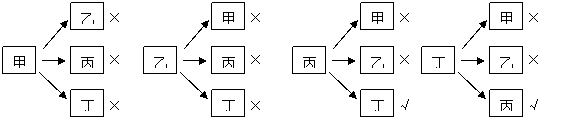

 .(列表方法求解略)·
.(列表方法求解略)·