摘要：如图.已知等边△ABC和点P.设点P到△ABC三边AB.AC.BC的距离分别为h1.h2.h3.△ABC的高为h． 在图(1)中. 点P是边BC的中点.此时h3=0.可得结论:． 在图中.点P分别在线段MC上.MC延长线上.△ABC内.△ABC外． 中. h1.h2.h3.h之间的关系, 所得结论, 所得结论． 中.若四边形RBCS是等腰梯形.∠B=∠C=60o. RS=n.BC=m.点P在梯形内.且点P到四边BR.RS.SC.CB的距离分别是h1.h2.h3.h4.桥形的高为h.则h1.h2.h3.h4.h之间的关系为: ,图中的等式有何关系? 解:(1)图②-⑤ 中的关系依次是: h1+h2+h3=h, h1-h2+h3=h, h1+h2+h3=h, h1+h2-h3=h． (2)图②中.h1+h2+h3=h． 证法一: ∵ h1=BPsin60o.h2=PCsin60o.h3=0. ∴ h1+h2+h3=BPsin60o+PCsin60o =BCsin60o=ACsin60o=h． 证法二:连结AP. 则SΔAPB+SΔAPC=SΔABC． ∴ ． 又 h3=0.AB=AC=BC. ∴ h1+h2+h3==h． (3)证明:图④中.h1+h2+h3=h． 过点P作RS∥BC与边AB.AC相交于R.S． 在△ARS中.由图②中结论知:h1+h2+0=h-h3． ∴ h1+h2+h3=h． 说明:问.通过作辅助线.利用证全等三角形的方法类似给分． (4)h1+h3+h4= ． 让R.S延BR.CS延长线向上平移.当n=0时.图⑥变为图④.上面的等式就是图④中的等式.所以上面结论是图④中结论的推广．
网址：http://m.1010jiajiao.com/timu3_id_457667[举报]
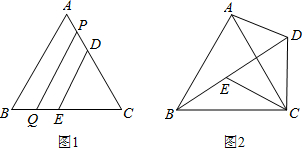
如图，已知等边△ABC和等边△CDE，P、Q分别为AD、BE的中点．
（1）试判断△CPQ的形状并说明理由．
（2）如果将等边△CDE绕点C旋转，在旋转过程中△CPQ的形状会改变吗？请你将图2中的图形补画完整并说明理由．
查看习题详情和答案>>
（1）试判断△CPQ的形状并说明理由．
（2）如果将等边△CDE绕点C旋转，在旋转过程中△CPQ的形状会改变吗？请你将图2中的图形补画完整并说明理由．
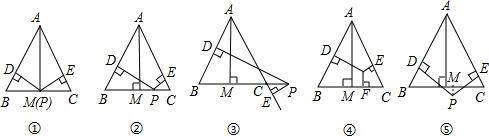
如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h．在图①中，点P是边BC的中点，由S△ABP+S△ACP=S△ABC得，
AB．h1+
AC．h2=
BC．h，可得h1+h2=h又因为h3=0，所以：h1+h2+h3=h．
图②～⑤中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图②～⑤中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）说明图②所得结论为什么是正确的；
（3）说明图⑤所得结论为什么是正确的．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
图②～⑤中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图②～⑤中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）说明图②所得结论为什么是正确的；
（3）说明图⑤所得结论为什么是正确的．
查看习题详情和答案>>
27、如图，已知等边△ABC和等边△DBC有公共的底边BC．
（1）以图1中的某个点为旋转中心，旋转△DBC，就能使△DBC与△ABC重合，则满足题意的点为
（2）如图2，已知B1是BC的中点，现沿着由点B到点B1的方向，将△DBC平移到△D1B1C1的位置．请你判断：得到的四边形ABD1C1是平行四边形吗？说明你的理由．
查看习题详情和答案>>
（1）以图1中的某个点为旋转中心，旋转△DBC，就能使△DBC与△ABC重合，则满足题意的点为
B点、C点、BC的中点
；（写出所有的这种点）（2）如图2，已知B1是BC的中点，现沿着由点B到点B1的方向，将△DBC平移到△D1B1C1的位置．请你判断：得到的四边形ABD1C1是平行四边形吗？说明你的理由．
（2007•临夏州）[（1）-（3），10分]如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h．
在图（1）中，点P是边BC的中点，此时h3=0，可得结论：h1+h2+h3=h．
在图（2）--（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图（2）--（5）中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）证明图（2）所得结论；
（3）证明图（4）所得结论．
（4）在图（6）中，若四边形RBCS是等腰梯形，∠B=∠C=60°，RS=n，BC=m，点P在梯形内，且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4，桥形的高为h，则h1、h2、h3、h4、h之间的关系为：
查看习题详情和答案>>
在图（1）中，点P是边BC的中点，此时h3=0，可得结论：h1+h2+h3=h．
在图（2）--（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图（2）--（5）中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）证明图（2）所得结论；
（3）证明图（4）所得结论．
（4）在图（6）中，若四边形RBCS是等腰梯形，∠B=∠C=60°，RS=n，BC=m，点P在梯形内，且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4，桥形的高为h，则h1、h2、h3、h4、h之间的关系为：
m（h1+h2+h3）-n（h1+h3-h4）=（m+n）h
m（h1+h2+h3）-n（h1+h3-h4）=（m+n）h
；图（4）与图（6）中的等式有何关系？
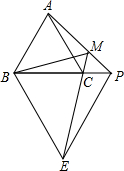如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于M，连BM，下列结论：①AP=CE；②∠PME=60°；③BM平分∠AME；④AM+MC=BM，其中正确的有