，
，
，
，且
，则实数x的值等于
A．
B．
C．
D．
∁UB B．
∁UB
C．∁UB D．∁UA
∁UB
．
(1)求f (1)的值；
(2)若a＞b＞c＞1，且a，b，c成等比数列，求证：
；
(3)若
，求证：f (x)在(0，+∞)上为增函数．21.
|
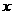轴于点P，交线段AB于点Q．
(1)试用t表示切线PQ的方程；
(2)设△QAP的面积为g (t)，若函数g (t)在(m，n)上单调递减，试求出m的最小值；
(3)当
，64]时，试求出点P横坐标的取值范围．
轴于点P，交线段AB于点Q．
(1)试用t表示切线PQ的方程；
(2)设△QAP的面积为g (t)，若函数g (t)在(m，n)上单调递减，试求出m的最小值；
(3)当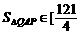，64]时，试求出点P横坐标的取值范围．
21.
|
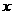轴于点P，交线段AB于点Q．
(1)试用t表示切线PQ的方程；
(2)设△QAP的面积为g (t)，若函数g (t)在(m，n)上单调递减，试求出m的最小值；
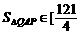(3)当，64]时，试求出点P横坐标的取值范围．
．
(1)求数列{an}的通项公式；
(2)若数列{cn}满足
，数列{cn}的前n项和为Tn，求Tn；
(3)张三同学利用第(2)题中的Tn设计了一个程序流程如图，但李四同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去，而无法结束)．你是否同意李四同学的观点？请说明理由．
，1)，
，0)，其中
＞0，又函数f (x) 
是以
为最小正周期的周期函数，当x∈[0，
]时，函数f (x)的最小值为－2．
(1)求f (x)的解析式；
(2)写出函数f (x)的单调递增区间；
(3)将函数f (x)的图象沿向量m平移后可以得到一个偶函数的图象，请写出一个符合条件的向量m．
的解集为M．
(1)当a = 4时，求集合M；
(2)若3
M且5
M，求实数a的取值范围．
，
，
，……，
(n∈N)，则f2006(x)
= ▲ ．