摘要:已知: 如图, 长方体AC1中, 棱AB=BC=3, 棱BB1=4, 连结B1C, 过点B作B1C的垂线交CC1于点E, 交B1C于点F. (1) 求证: A1C平面EBD; (2) 求点A到平面A1B1C的距离; (3) 求ED与平面A1B1C所成角的大小. 解: (1)连结AC.在长方体AC1中, A1C在底面ABCD上的射影为AC, AC⊥BD, ∴AC1⊥BD. -- 在长方体AC1中, A1C在平面BB1C1C上的射影为B1C,B1C⊥BE, ∴A1C⊥BE. -- 又BDBE=B, ∴A1C⊥平面EBD. -- (2) ∵BF⊥B1C, BF⊥AB1, B1CA1B1=B1, ∴BF⊥平面A1B1C1, -- 又∵A1B1∥AB, A1B1平面A1B1C,AB平面A1B1C, ∴AB∥平面A1B1C, 点A到平面A1B1C的距离即为点 B到平面A1B1C距离, 也就是BF. -- 在△B1BC中, 易知, 点A到平面A1B1C的距离为.-- (3)连结A1D.FD. 由(2)知BE⊥平面A1B1C, 即BE⊥平面A1B1CD, ∴∠EDF为ED与平面A1B1C所成的角. -- 矩形B1BCC1中, 易求得B1F=, CF=, EF= EC= 又在Rt△CDE中, ,-- 即ED与平面A1B1C所成角为.--
网址:http://m.1010jiajiao.com/timu3_id_4471447[举报]
 (1)求
(1)求 的定义域;(2)求
的定义域;(2)求 .
. 时,求函数
时,求函数 的单调递减区间;
的单调递减区间; 时,
时, 上恒大于0,求实数
上恒大于0,求实数 的取值范围.
的取值范围. 的图像关于原点对称,并且当
的图像关于原点对称,并且当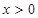 时,
时, ,试求
,试求 上的表达式,并画出它的图像,根据图像写出它的单调区间。
上的表达式,并画出它的图像,根据图像写出它的单调区间。 的不等式
的不等式 ,其中
,其中 .
. 变化时,试求不等式的解集
变化时,试求不等式的解集 ;
;  (其中
(其中 为整数集). 试探究集合
为整数集). 试探究集合 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合
 关于点
关于点 对称.
对称. 的值.
的值.