0 447064 447072 447078 447082 447088 447090 447094 447100 447102 447108 447114 447118 447120 447124 447130 447132 447138 447142 447144 447148 447150 447154 447156 447158 447159 447160 447162 447163 447164 447166 447168 447172 447174 447178 447180 447184 447190 447192 447198 447202 447204 447208 447214 447220 447222 447228 447232 447234 447240 447244 447250 447258 447348
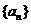 的通项公式为
的通项公式为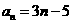 ,则
,则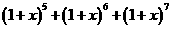 的展开式中含
的展开式中含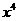 项的系数是该数列的 ( )
项的系数是该数列的 ( )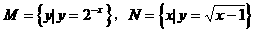 ,则
,则 ( )
( )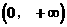 B.
B.
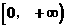
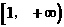 D.
D.
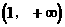
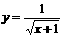 的定义域是 ( )
的定义域是 ( )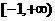 B.
B.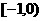 C.
C.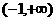 D.(-1,0)
D.(-1,0) 所对应的点在 ( )
所对应的点在 ( )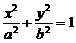 过点
过点 ,
,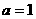 . ………………………………………………………………………………………………………………1分
. ………………………………………………………………………………………………………………1分 ,
,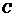 横坐标适合方程
横坐标适合方程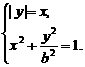
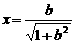 (
(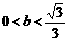 即
即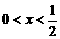 ).………………………………………………………4分
).………………………………………………………4分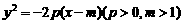 . …………………6分
. …………………6分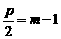 ,∴
,∴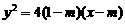 .………………………………………………………………7分
.………………………………………………………………7分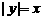 和
和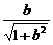 ,
,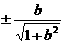 ))代入式抛物线方
))代入式抛物线方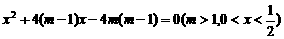 . ……………………………………9分
. ……………………………………9分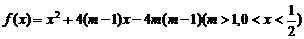 .……………………………………10分
.……………………………………10分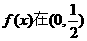 内有根(并且是单调递增函数),
内有根(并且是单调递增函数),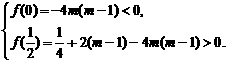 ………………………………………………………………13分
………………………………………………………………13分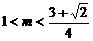 . …………………………………………………………………………………………14分
. …………………………………………………………………………………………14分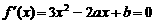 有解,
有解,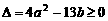 即
即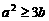 . ……………………………………………………………………………3分
. ……………………………………………………………………………3分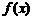 可以在
可以在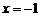 和
和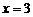 时取得极值,
时取得极值,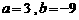 . ………………………………………………………………………………………………6分
. ………………………………………………………………………………………………6分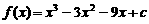 . ………………………………………………………………7分
. ………………………………………………………………7分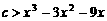 (
(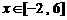 )恒成立. ……………………………………………9分
)恒成立. ……………………………………………9分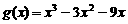 (
(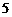 (用求导的方法),
(用求导的方法),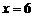 处的值为
处的值为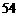 .
. 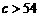 . …………………………………………………………………………………………………………14分
. …………………………………………………………………………………………………………14分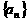 的公差为
的公差为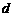 ,则
,则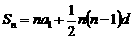 …………… 2分
…………… 2分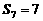 ,
,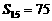 ,
,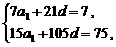 即
即
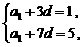 ……………
4分
……………
4分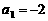 ,
,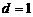 。……………………………………………… 6分
。……………………………………………… 6分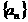 的通项公式为
的通项公式为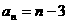 …………………… 7分
…………………… 7分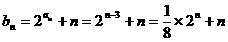 ………………………… 9分
………………………… 9分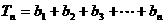
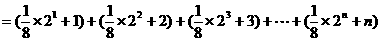
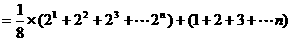
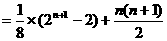
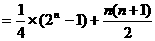
 证明:∵
证明:∵ 是菱形,
是菱形,  ∴
∴  ⊥
⊥ ……………………..1分
……………………..1分  ,且
,且
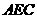 , ……………………..3分
, ……………………..3分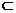 平面
平面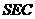

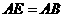 ,
,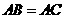 ∴
∴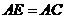
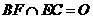
 的中点
的中点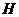 ,连结
,连结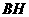 、
、
 ∵
∵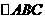 是等边三角形 ∴
是等边三角形 ∴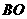 ⊥平面
⊥平面 上的射影,∴由三垂线定理逆定理 可得
上的射影,∴由三垂线定理逆定理 可得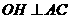
 是二面角
是二面角 的平面角 ……………7分
的平面角 ……………7分 ≌Rt
≌Rt ,则
,则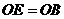 ,∴四边形
,∴四边形 中,
中,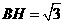 ,
,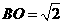 ∴
∴ =
=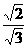 =
=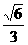 ………9分
………9分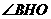 =arcsin
=arcsin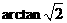 ,
,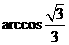 )
) 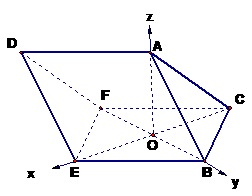 另解:由(Ⅰ)易证
另解:由(Ⅰ)易证 为原点,
为原点, 轴,
轴, 轴, OA所在直线为
轴, OA所在直线为 轴,建立空间直角坐标系(如图),则A(0,0,
轴,建立空间直角坐标系(如图),则A(0,0,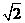 ), B(0,
), B(0, 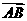 =(0,
=(0,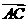 =(-
=(-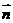 =(
=(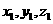 )为平面
)为平面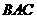 的法向量,则
的法向量,则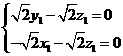
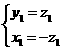 ,取
,取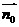 =(-1,1,1)为平面
=(-1,1,1)为平面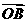 =(0,
=(0,  的一个法向量。设
的一个法向量。设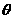 为
为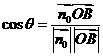 =
=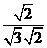 =
=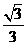 ………………………………………………………….9分
………………………………………………………….9分 ∥
∥ ,
,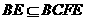

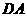 ∥平面
∥平面 、
、 到面
到面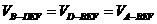 …………………………………………………………………..12分
…………………………………………………………………..12分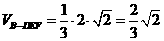 …………………………………………………………14分
…………………………………………………………14分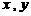 是随机变量.
是随机变量.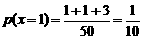 .
.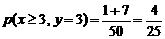 . …………………………………6分
. …………………………………6分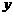 的期望为
的期望为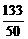 ,得
,得 ,即
,即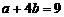 . …………………9分
. …………………9分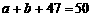 ,即
,即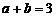 . ………………………………………………11分
. ………………………………………………11分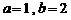 . …………………………………………………………………………………………12分
. …………………………………………………………………………………………12分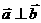 解:(1)
解:(1)  ∵
∵
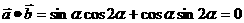 ∴
……………………………………………… 2分
∴
……………………………………………… 2分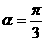
 即
…………………………………………… 4分
即
…………………………………………… 4分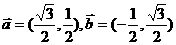
 ∴
∴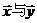 设向量
的夹角为θ
设向量
的夹角为θ 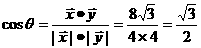 则
则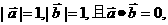 解法二:
解法二: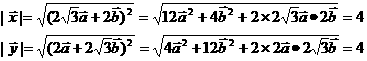 由已知可得
………………………………… 7分
由已知可得
………………………………… 7分