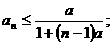4.
设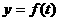 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中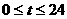 .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观观察,函数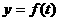 的图象可以近似地看成函数
的图象可以近似地看成函数 的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
(A)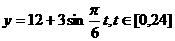 (B)
(B)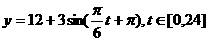
(C)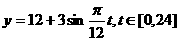 (D)
(D)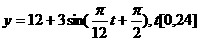
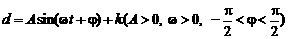 ,且当P点从水面上浮现时开始计算时间.有以下四个结论:
,且当P点从水面上浮现时开始计算时间.有以下四个结论: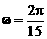 ; ③
; ③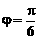 ; ④k=5.
; ④k=5.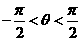 ,且
,且 其中
其中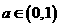 ,则关于
,则关于 的值,在以下四个答案中,可能正确的是 ( )
的值,在以下四个答案中,可能正确的是 ( )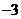 (B)3 或
(B)3 或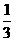
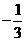 (D)
(D)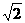 (B)20
(B)20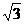 (C)40
(C)40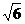
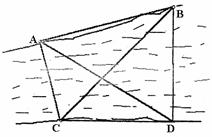
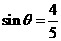 ,且
,且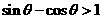 ,则
,则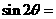 ( )
( )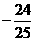 (B)
(B)
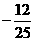 (C)
(C)
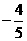 (D)
(D) 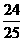
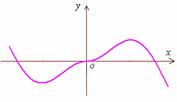
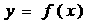 的图象如图所示,则
的图象如图所示,则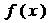 的解析式可能是
( )
的解析式可能是
( )
 (A)
(A)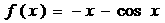
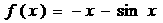
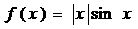
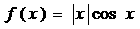
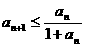 变形,得
变形,得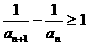 .
.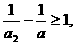
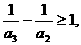
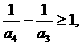
 .
.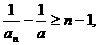
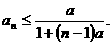
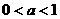 ,于是由(1)得
,于是由(1)得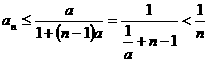 ,
,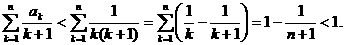
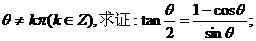
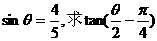 的值.
的值.
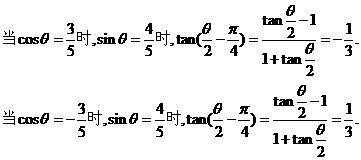
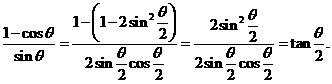
 .
.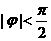 )
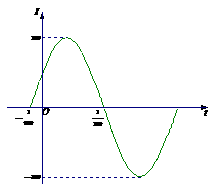
)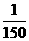 秒的时间内,电流
秒的时间内,电流 ,t2=
,t2=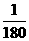 , 则周期T=2(t2-t1)=2(
, 则周期T=2(t2-t1)=2(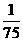 .
.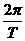 =150π.
=150π.
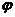 )=0,
)=0,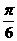 .
.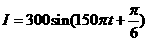 .
.
 ≤
≤ .
.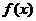 的最大值及取得最大值时x的值.
的最大值及取得最大值时x的值.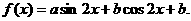

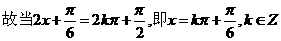 时,函数f(x)的最大值为12.
时,函数f(x)的最大值为12.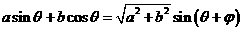 是历年高考命题的热点之一.
是历年高考命题的热点之一.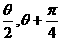 ,可向
,可向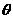 角转化,以便出现
角转化,以便出现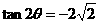 可向
可向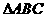 中,
中,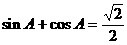 ,
,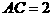 ,
,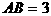 ,求
,求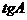 的值和
的值和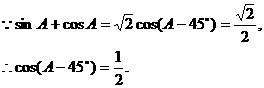
 ,
,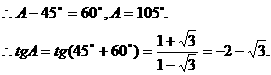
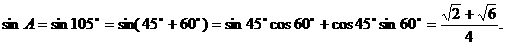
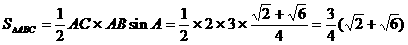 .
.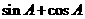 计算它的对偶关系式
计算它的对偶关系式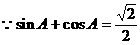 ①
①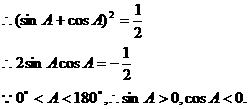
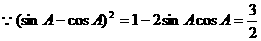 ,
,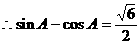 . ②
. ②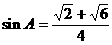 .
.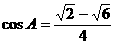 .
.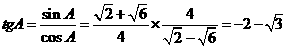 .以下解法略去.
.以下解法略去.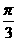 ,
,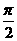 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.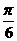 ).
).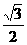 .
. 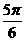 ,
,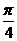 .
.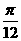 )+1.
)+1.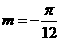 ,
,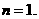
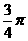 ,且m·n=-1.
,且m·n=-1.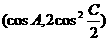 ,其中A、C为△ABC的内角,且A、B、C依次成等差数列.求|n+p|的取值范围.
,其中A、C为△ABC的内角,且A、B、C依次成等差数列.求|n+p|的取值范围.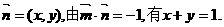 ①
① 与
与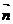 夹角为
夹角为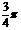 ,有
,有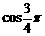 ,
,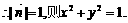 ②
②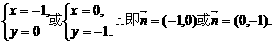
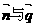 垂直知
垂直知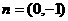 ,
,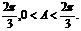

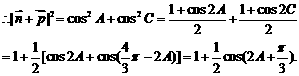
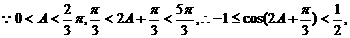
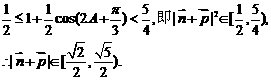
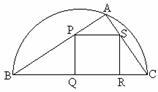 (2)当a固定,
(2)当a固定,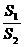 取最小值时的角
取最小值时的角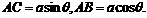
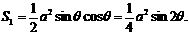
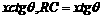
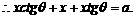
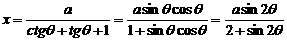
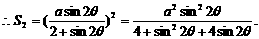
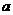 固定,
固定,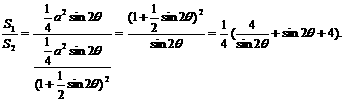
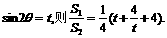
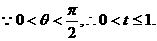 令
令 任取
任取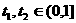 ,且
,且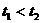 ,
,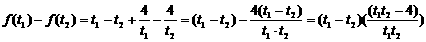 .
. ,
,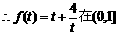 是减函数.
是减函数.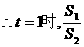 取最小值,此时
取最小值,此时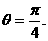
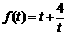 .这些解题思维的拐点,你能否很快的想到呢?
.这些解题思维的拐点,你能否很快的想到呢? 亩,但当年实际沙地面积为24000亩,所以1999年沙化土地为200亩.
亩,但当年实际沙地面积为24000亩,所以1999年沙化土地为200亩. 、
、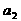 、
、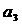 、…,则n年造林面积总和为:
、…,则n年造林面积总和为: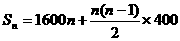 .
. 化简得
化简得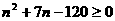 ,
, .
.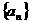 满足
满足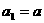 (
(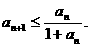 求证
求证