0 446834 446842 446848 446852 446858 446860 446864 446870 446872 446878 446884 446888 446890 446894 446900 446902 446908 446912 446914 446918 446920 446924 446926 446928 446929 446930 446932 446933 446934 446936 446938 446942 446944 446948 446950 446954 446960 446962 446968 446972 446974 446978 446984 446990 446992 446998 447002 447004 447010 447014 447020 447028 447348
 }的前n项和
}的前n项和 其中a、b是非零常数,则存在数列{
其中a、b是非零常数,则存在数列{ }、{
}、{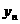 }使得
}使得  为等差数列,{
为等差数列,{ 为等差数列,{
为等差数列,{ 上的最大值和最小值之和为a,则a的值为
上的最大值和最小值之和为a,则a的值为 (B)
(B)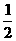 (C)2 (D)4
(C)2 (D)4 的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为
的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为  (B)3 (C)
(B)3 (C)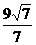 (D)
(D)
 ,则下列不等式①
,则下列不等式① ;②
;② ③
③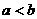 ;④
;④ 中,正确的不等式有
中,正确的不等式有  为非零的平面向量. 甲:
为非零的平面向量. 甲:
 的解析式可取为
的解析式可取为 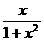 (B)
(B) (C)
(C) (D)
(D)
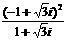 的值是
的值是  (D)
(D)
 的平行的抛物线
的平行的抛物线 的切线方程是
的切线方程是 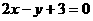 (B)
(B)
 (D)
(D)
 (18)(12分)如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2. E、F分别是线段AB、BC上的点,且EB= FB=1.
(18)(12分)如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2. E、F分别是线段AB、BC上的点,且EB= FB=1.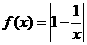 (x>0).
(x>0).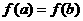 时,ab>1;
时,ab>1;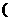 0<x0<1
0<x0<1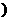 在曲线
在曲线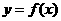 上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达). ,其中常数m为整数.
,其中常数m为整数. ≥0;
≥0;  相交于A、B两点,l又与双曲线x2-y2=1相交于C、D两点,C、D三等分线段AB.求直线l的方程.
相交于A、B两点,l又与双曲线x2-y2=1相交于C、D两点,C、D三等分线段AB.求直线l的方程. (15)由图(1)有面积关系:
(15)由图(1)有面积关系: ,则由图(2)有体积关系:
,则由图(2)有体积关系: =
.
=
. (x>0)的反函数
(x>0)的反函数 =
.
=
.