摘要：20． 已知函数的图象过点P(0.2).且在点M(-1.f(-1))处的切线方程为. (Ⅰ)求函数的解析式, (Ⅱ)求函数的单调区间. 解:(Ⅰ)由的图象过点P(0.2),d=2知,所以 ,(x)=3x2+2bx+c,由在处的切线方程是6x-y+7=0,知 -6-f=1, (-1)=6,∴即解得b=c=-3. 故所求的解析式为f(x)=x3-3x-3+2, (Ⅱ) (x)=3x2-6x-3,令3x2-6x-3=0即x2-2x-1=0,解得x1=1-,x2=1+, 当x<1-或x>1+时, (x)>0;当1-<x<1+时, (x)<0 ∴f(x)=x3-3x2-3x+2在(1+,+∞)内是增函数,在(-∞, 1-)内是增函数,在(1-,1+)内是减函数.
网址：http://m.1010jiajiao.com/timu3_id_4469087[举报]
的部分图象如图所示.
的解析式；
（2） 如何由函数
的图象通过适当的变换得到函
，求
的值.
已知函数 的最大值是2，其图象经过点
．
的解析式；
，且
，
的值．(本小题满分12分)
已知函数f(x)＝lg(ax－bx)(a>1>b>0)．
(1)求y＝f(x)的定义域；
(2)在函数y＝f(x)的图象上是否存在不同的两点，使得过这两点的直线平行于x轴；
(3)当a，b满足什么条件时，f(x)在(1，＋∞)上恒取正值．
查看习题详情和答案>>
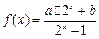的反函数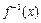
的图象过点
．
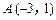的值；