摘要：22． 已知方向向量为的直线l过点()和椭圆的焦点.且椭圆C的中心关于直线l的对称点在椭圆C的右准线上. (Ⅰ)求椭圆C的方程, (Ⅱ)是否存在过点E的直线m交椭圆C于点M.N.满足cot ∠MON≠0.若存在.求直线m的方程,若不存在.请说明理由. 解:(Ⅰ)由题意可得直线ι:, ① 过原点垂直ι的方程为 ② 解①②得x=.∵椭圆中心O(0,0)关于直线ι的对称点在椭圆C的右准线上, ∴.∵直线ι过椭圆焦点,∴该焦点坐标为(2,0). ∴a2=6,c=2,b2=2,故椭圆C的方程为. ③ (Ⅱ)设M(x1,y1),N(x2,y2),当直线m不垂直x轴时,直线m:y=k(x+2)代入③,整理得 (3k2+1)x2+12k2x+12k2-6=0,则x1+x2=,x1x2=, |MN|= 点O到直线MN的距离d=.∵cot∠MON,即 , ∴,∴, 即.整理得. 当直线m垂直x轴时,也满足 故直线m的方程为或y=或x=-2. 经检验上述直线均满足. 所在所求直线方程为或y=或x=-2..
网址：http://m.1010jiajiao.com/timu3_id_4469089[举报]
（本小题满分14分）
（1）（矩阵与变换）已知二阶矩阵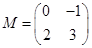
（Ⅰ）求矩阵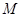
的
逆矩阵；
（Ⅱ）设向量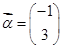
，求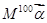
（2）（坐标系与参数方程）
已知曲线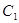
的参数方程为
（
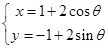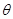是参数），曲线
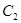的极坐标方程为
（
．
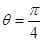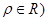（Ⅰ）
求曲线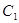的普通方程和曲线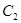的平面直角坐标方程
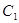（Ⅱ）设曲线和曲线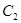相交于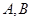
两点，求弦长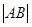
查看习题详情和答案>>
（本小题满分14分）
设
是椭圆
上的两点，已知向量
且
，椭圆的离心率
短轴长为2，
为坐标原点。
（1）求椭圆的方程；
（2）若直线AB的斜率存在且直线AB过椭圆的焦点F（0，c），（c为半焦距），求直线AB的斜率k的值；
（3）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.
查看习题详情和答案>>（本小题满分14分）
在平面直角坐标系中，已知向量
（
），
，动点
的轨迹为
．
（1）求轨迹的方程,并说明该方程表示的曲线的形状；
（2）当
时，已知点
，是否存在直线
：
，使点B关于直线的对称点落在轨迹上?若存在，求出直线的方程，若不存在，请说明理由.
的
逆矩阵；
，求
的参数方程为
（
是参数），曲线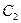
的极坐标方程为
（
．
求曲线
（Ⅱ）设曲线
两点，求弦长
的长、短轴端点分别为A、B，从此椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点
，向量
与
是共线向量．且椭圆长轴长为2
，