( 15 )(本小题满分12分)
化简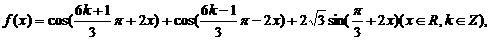 并求函数
并求函数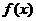 的值域和最小正周期.
的值域和最小正周期.
[答案]
解: 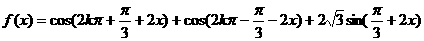
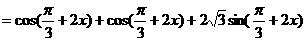
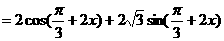
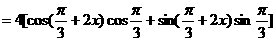

∴ 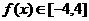 ,
,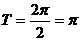 ,
,
∴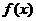 的值域是
的值域是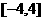 ,最小正周期是
,最小正周期是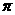 .
.
 ( 16 ) (本小题共14分)
( 16 ) (本小题共14分)
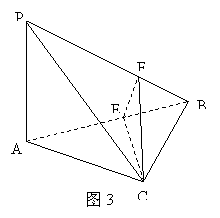
如图3所示,在四面体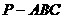 中,已知
中,已知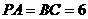 ,
,
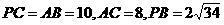 .
.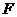 是线段
是线段 上一点,
上一点,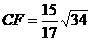 ,点
,点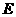 在线段
在线段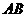 上,且
上,且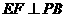 .
.
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的大小.
的大小.
[答案]
(Ⅰ)证明:在 中, ∵
中, ∵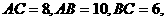
∴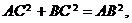
∴△PAC是以∠PAC为直角的直角三角形,
同理可证,△PAB是以∠PAB为直角的直角三角形,
△PCB是以∠PCB为直角的直角三角形.
在 中,∵
中,∵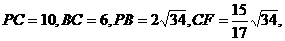
∴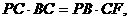 ∴
∴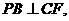
又∵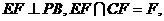
∴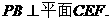
(II)
解法一:由(I)知PB⊥CE,PA⊥平面ABC
∴AB是PB在平面ABC上的射影,故AB⊥CE
∴CE⊥平面PAB,而EF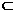 平面PAB,
平面PAB,
∴EF⊥EC,
故∠FEB是二面角B-CE-F的平面角,
∵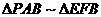
∴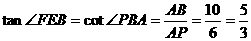 ,
,
∴二面角B-CE-F的大小为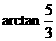 .
.
解法二:如图,以C点的原点,CB、CA为x、y轴,
建立空间直角坐标系C-xyz,则
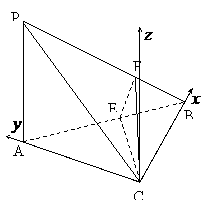
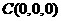 ,
,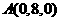 ,
,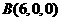 ,
,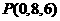 ,
,
∵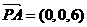 为平面ABC的法向量,
为平面ABC的法向量,
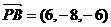 为平面ABC的法向量,
为平面ABC的法向量,
∴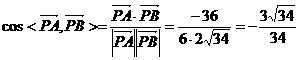 ,
,
∴二面角B-CE-F的大小为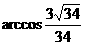 .
.
|
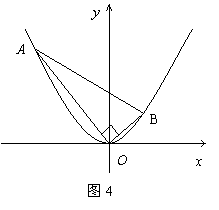 在平面直角坐标系
在平面直角坐标系 中,抛物线
中,抛物线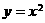 上异于坐标原点
上异于坐标原点 的两不同动点A、B满足
的两不同动点A、B满足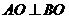 (如图4所示)
(如图4所示)
(Ⅰ)求 得重心
得重心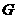 (即三角形三条中线的交点)
(即三角形三条中线的交点)
的轨迹方程;
(Ⅱ) 的面积是否存在最小值?若存在,请求出
的面积是否存在最小值?若存在,请求出
最小值;若不存在,请说明理由.
[答案]
解法一:
(Ⅰ)∵直线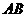 的斜率显然存在,∴设直线
的斜率显然存在,∴设直线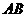 的方程为
的方程为 ,
,
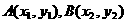 ,依题意得
,依题意得
 ,①
,①
∴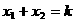 ,②
,② 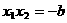 ③
③
∵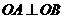 ,∴
,∴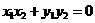 ,即
,即 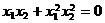 ,④
,④
由③④得,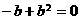 ,∴
,∴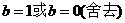
∴设直线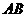 的方程为
的方程为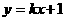
∴①可化为  ,∴
,∴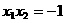 ⑤,
⑤,
设 的重心G为
的重心G为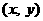 ,则
,则
 ⑥ ,
⑥ , 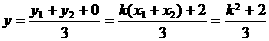 ⑦,
⑦,
由⑥⑦得 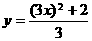 ,即
,即 ,这就是
,这就是 得重心
得重心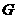 的轨迹方程.
的轨迹方程.
(Ⅱ)由弦长公式得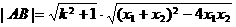
把②⑤代入上式,得 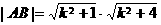 ,
,
设点 到直线
到直线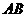 的距离为
的距离为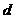 ,则
,则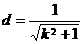 ,
,
∴ 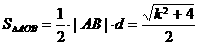 ,
,
∴ 当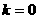 ,
,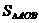 有最小值,
有最小值,
∴ 的面积存在最小值,最小值是
的面积存在最小值,最小值是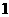 .
.
解法二:
(Ⅰ)∵ AO⊥BO, 直线 ,
,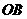 的斜率显然存在,
的斜率显然存在,
∴设AO、BO的直线方程分别为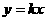 ,
,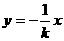 ,
,
设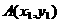 ,
,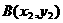 ,依题意可得
,依题意可得
由 得
得 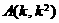 ,由
,由 得
得 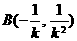 ,
,
设 的重心G为
的重心G为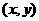 ,则
,则
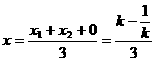 ① ,
① , 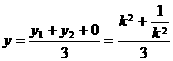 ②,
②,
由①②可得, ,即为所求的轨迹方程.
,即为所求的轨迹方程.
(Ⅱ)由(Ⅰ)得,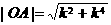 ,
,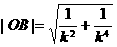 ,
,
∴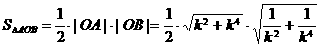
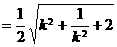
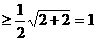 ,
,
当且仅当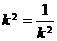 ,即
,即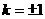 时,
时,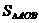 有最小值,
有最小值,
∴ 的面积存在最小值,最小值是
的面积存在最小值,最小值是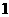 .
.
解法三:(I)设△AOB的重心为G(x , y) ,A(x1, y1),B(x2 , y2 ),则
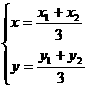 …(1)
…(1)
不过∵OA⊥OB ,
∴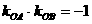 ,即
,即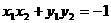 , …(2)
, …(2)
又点A,B在抛物线上,有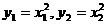 ,
,
代入(2)化简得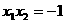 ,
,
∴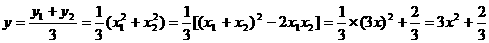 ,
,
∴所以重心为G的轨迹方程为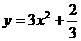 ,
,
(II)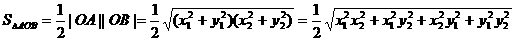 ,
,
由(I)得 ,
,
当且仅当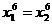 即
即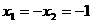 时,等号成立,
时,等号成立,
所以△AOB的面积存在最小值,存在时求最小值1 .
( 18 ) (本小题共12分)
箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为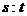 .现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次.以
.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次.以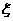 表示取球结束时已取到白球的次数.
表示取球结束时已取到白球的次数.
(Ⅰ)求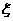 的分布列;
的分布列;
(Ⅱ)求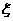 的数学期望.
的数学期望.
[答案]
解:(Ⅰ)取出黄球的概率是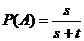 ,取出白球的概率是
,取出白球的概率是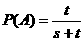 ,则
,则
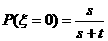 ,
, 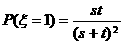 ,
, 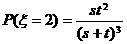 ,
,
……, 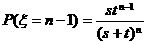 ,
, 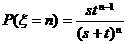 ,
,
∴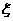 的分布列是
的分布列是
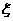 |
0 |
1 |
2 |
… |
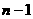 |
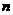 |
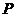 |
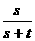 |
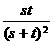 |
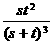 |
… |
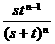 |
 |
(Ⅱ)
 …
…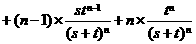 ①
①
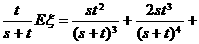 …
…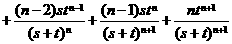 ②
②
①-②得
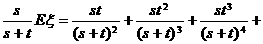 …
…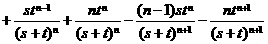
∴ 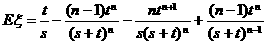
∴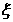 的数学期望是
的数学期望是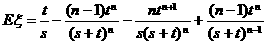 .
.
( 19 ) (本小题共14分)
设函数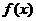 在
在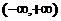 上满足
上满足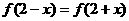 ,
,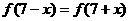 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有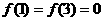 .
.
(Ⅰ)试判断函数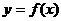 的奇偶性;
的奇偶性;
(Ⅱ)试求方程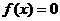 在闭区间
在闭区间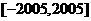 上的根的个数,并证明你的结论.
上的根的个数,并证明你的结论.
[答案]
解:(Ⅰ)∵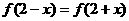 ,
,
∴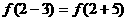
即 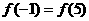 ,
,
∵在[0,7]上,只有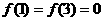 ,
,
∴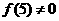 ,∴
,∴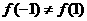 ,
,
∴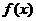 是非奇非偶函数.
是非奇非偶函数.
(Ⅱ)由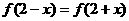 ,令
,令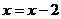 ,得
,得 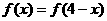 ,
,
由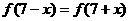 ,令
,令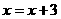 ,得
,得 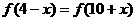 ,
,
∴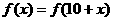 ,
,
∴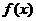 是以10为周期的周期函数,
是以10为周期的周期函数,
由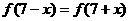 得,
得,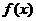 的图象关于
的图象关于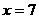 对称,
对称,
∴在[0,11]上,只有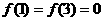 ,
,
∴10是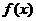 的最小正周期,
的最小正周期,
∵在[0,10]上,只有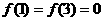 ,
,
∴在每一个最小正周期内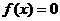 只有两个根,
只有两个根,
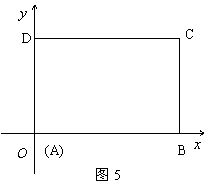
∴在闭区间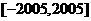 上的根的个数是
上的根的个数是 .
.
 ( 20 ) (本小题共14分)
( 20 ) (本小题共14分)
在平面直角坐标系中,已知矩形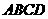 的长为2,宽为1,
的长为2,宽为1,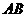 、
、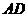 边分别在
边分别在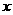 轴、
轴、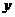 轴的正半轴上,
轴的正半轴上, 点与坐标原点重合(如图5所示).将矩形折叠,使
点与坐标原点重合(如图5所示).将矩形折叠,使 点落在线段
点落在线段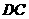 上.
上.
(Ⅰ)若折痕所在直线的斜率为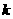 ,试写出折痕所在直线的方程;
,试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.
[答案]
解:(Ⅰ)( i ) 当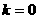 时,此时A点与D点重合, 折痕所在的直线方程
时,此时A点与D点重合, 折痕所在的直线方程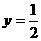 ,
,
( ii ) 当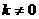 时,设A点落在线段
时,设A点落在线段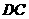 上的点
上的点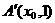 ,
,
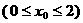 ,则直线
,则直线 的斜率
的斜率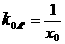 ,
,
∵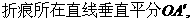
∴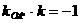 ,∴
,∴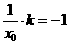 ,∴
,∴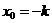
又∵折痕所在的直线与 的交点坐标(线段
的交点坐标(线段 的中点)
的中点)
为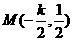 ,
,
∴折痕所在的直线方程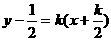 ,即
,即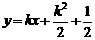 ,
,
由( i ) ( ii )得折痕所在的直线方程为: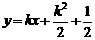
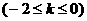
(Ⅱ)折痕所在的直线与坐标轴的交点坐标为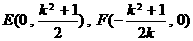
由(Ⅰ)知,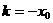 ,∵
,∵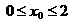 ,∴
,∴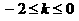 ,
,
设折痕长度为d,所在直线的倾斜角为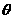 ,
,
( i ) 当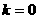 时,此时A点与D点重合, 折痕的长为2 ;
时,此时A点与D点重合, 折痕的长为2 ;
( ii )当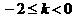 时,
时,
设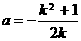 ,
,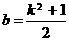 ,
,
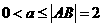 时,l与线段AB相交,此时
时,l与线段AB相交,此时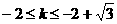 ,
,
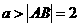 时,l与线段BC相交,此时
时,l与线段BC相交,此时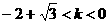 ,
,
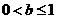 时,l与线段AD相交,此时
时,l与线段AD相交,此时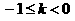 ,
,
 时,l与线段DC相交,此时
时,l与线段DC相交,此时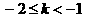 ,
,
∴将k所在的分为3个子区间:
①当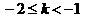 时,折痕所在的直线l与线段DC、AB相交,
时,折痕所在的直线l与线段DC、AB相交,
折痕的长 ,
,
∴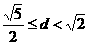 ,
,
②当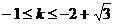 时,折痕所在的直线l与线段AD、AB相交,
时,折痕所在的直线l与线段AD、AB相交,
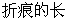
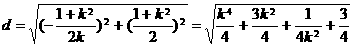
令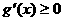 ,即
,即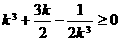 ,即
,即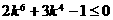 ,
,
即 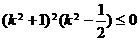 ,
,
∵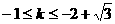 ,∴解得
,∴解得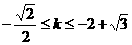
令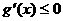 , 解得
, 解得 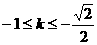 ,
,
故当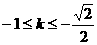 时,
时,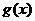 是减函数,当
是减函数,当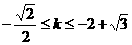 时,
时,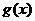 是增函数,
是增函数,
∵ ,
,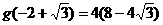 ,
,
∴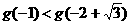 ,
,
∴当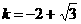 时,
时,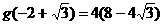 ,
,
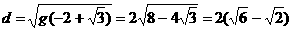 ,
,
∴当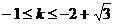 时,
时,  ,
,
③当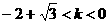 时,折痕所在的直线l与线段AD、BC相交,
时,折痕所在的直线l与线段AD、BC相交,
折痕的长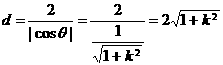 ,
,
∴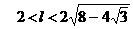 ,即
,即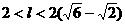 ,
,
综上所述得,当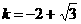 时,折痕的长有最大值,为
时,折痕的长有最大值,为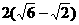 .
.
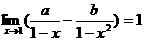 ,则常数
,则常数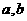 的值为 ( )
的值为 ( )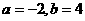 B.
B.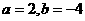 C.
C. D.
D.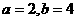
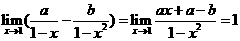 ,令a-b=--a,这时
,令a-b=--a,这时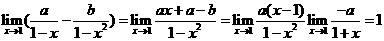 ,∴a=-2,由此得b=-4,选(C)
,∴a=-2,由此得b=-4,选(C)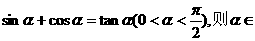 ( )
( )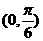 B.
B.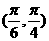 C.
C.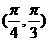 D.
D.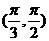
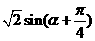 ∈(1,
∈(1,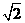 ),∴排除(A),(B),当α=
),∴排除(A),(B),当α=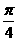 时,tanα=1,sinα+cosα=
时,tanα=1,sinα+cosα=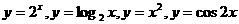 这四个函数中,当
这四个函数中,当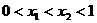 时,使
时,使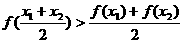 恒成立的函数的个数是 ( )
恒成立的函数的个数是 ( )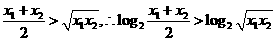 ,即当
,即当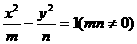 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线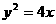 的焦点重合,则mn的值为 ( )
的焦点重合,则mn的值为 ( )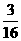 B.
B.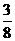 C.
C.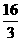 D.
D.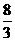
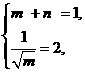 得m=
得m=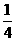 ,n=
,n=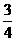 ,∴mn=
,∴mn=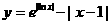 的图象大致是 ( )
的图象大致是 ( )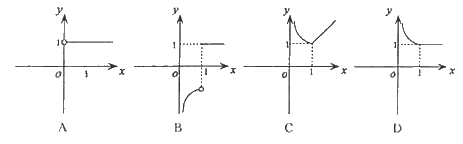
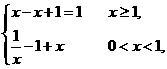 选(D)
选(D)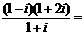 ( )
( )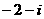 B.
B.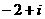 C.
C.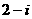 D.
D.
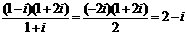 ,选(C)
,选(C)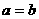 ”是“
”是“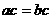 ”充要条件; ②“
”充要条件; ②“ 是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.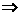 “a<5”,选(B)
“a<5”,选(B)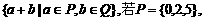
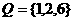 ,则P+Q中元素的个数是 ( )
,则P+Q中元素的个数是 ( )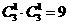 其对应的和有一个重复:0+6=1+5,
其对应的和有一个重复:0+6=1+5,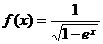 的定义域是
.
的定义域是
.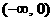
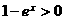 ,
, 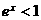 ,∴
,∴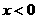 ,
,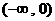 .
.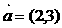 ,
,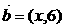 ,且
,且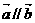 ,则
,则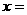 .
.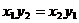 ,∴
,∴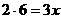 ,∴
,∴ .
.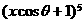 的展开式中
的展开式中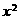 的系数与
的系数与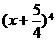 的展开式中
的展开式中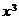 的系数相等,则
的系数相等,则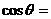
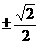
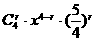 ,
,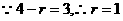 ,
,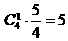 ,
,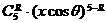 ,
,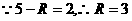 ,
,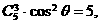
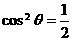 ,
,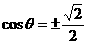 .
.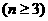 ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用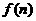 表示这
表示这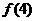 =____________;当
=____________;当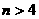 时,
时,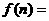 .(用
.(用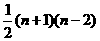
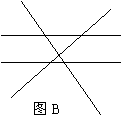 解:由图B可得
解:由图B可得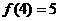 ,
,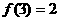 ,
,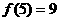 ,
,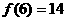 ,可推得
,可推得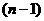 个,
个,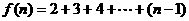
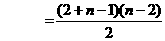
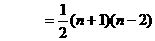 .
.