(17)(本大题满分12分)已知
(Ⅰ)求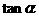 的值;
的值;
(Ⅱ)求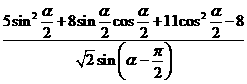 的值。
的值。
解:(Ⅰ)由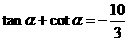 得
得 ,即
,即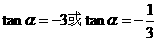 ,又
,又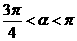 ,所以
,所以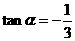 为所求。
为所求。
(Ⅱ)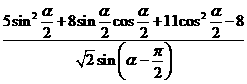 =
=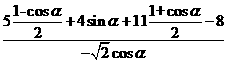
=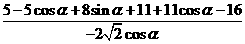 =
=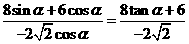 =
= 。
。
(18)(本大题满分12分)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用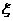 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出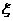 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求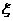 的数学期望
的数学期望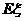 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)
解:(Ⅰ)
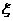 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
P |
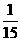 |
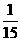 |
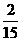 |
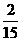 |
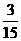 |
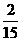 |
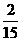 |
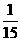 |
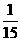 |
 (Ⅱ)
(Ⅱ)
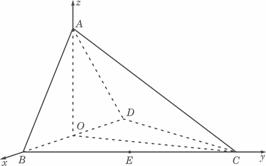
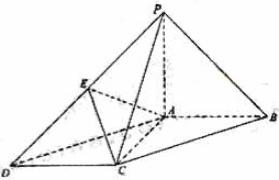
(19)(本大题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点,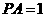 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明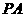 ⊥
⊥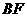 ;
;
(Ⅱ)求面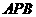 与面
与面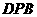 所成二面角的大小。
所成二面角的大小。
解:(Ⅰ)在正六边形ABCDEF中,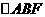 为等腰三角形,
为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;又∵正六边形ABCDEF的边长为1,∴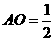 ,
,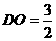 ,
,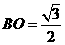 。
。
过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,所以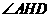 为所求二面角平面角。
为所求二面角平面角。
在 中,OH=
中,OH=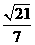 ,
,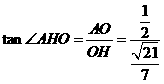 =
=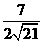 。
。
在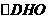 中,
中,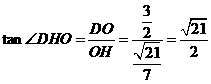 ;
;
而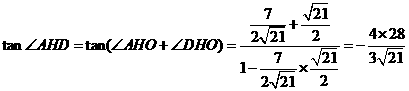
(Ⅱ)以O为坐标原点,建立空间直角坐标系,P(0,0,1),A(0, ,0),B(
,0),B( ,0,0),D(0,2,0),∴
,0,0),D(0,2,0),∴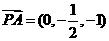 ,
,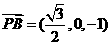 ,
,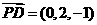
设平面PAB的法向量为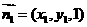 ,则
,则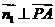 ,
,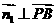 ,得
,得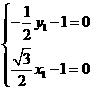 ,
,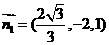 ;
;
设平面PDB的法向量为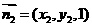 ,则
,则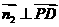 ,
,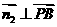 ,得
,得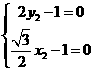 ,
,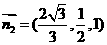 ;
;
(20)(本大题满分12分)已知函数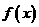 在R上有定义,对任何实数
在R上有定义,对任何实数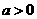 和任何实数
和任何实数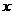 ,都有
,都有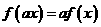
(Ⅰ)证明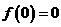 ;(Ⅱ)证明
;(Ⅱ)证明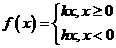 其中
其中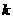 和
和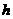 均为常数;
均为常数;
(Ⅲ)当(Ⅱ)中的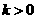 时,设
时,设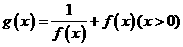 ,讨论
,讨论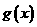 在
在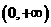 内的单调性并求极值。
内的单调性并求极值。
证明(Ⅰ)令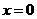 ,则
,则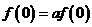 ,∵
,∵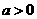 ,∴
,∴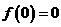 。
。
(Ⅱ)①令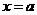 ,∵
,∵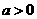 ,∴
,∴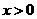 ,则
,则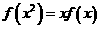 。
。
假设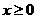 时,
时,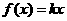
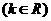 ,则
,则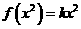 ,而
,而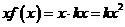 ,∴
,∴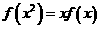 ,即
,即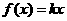 成立。
成立。
②令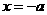 ,∵
,∵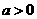 ,∴
,∴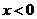 ,
,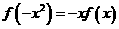
假设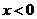 时,
时,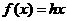
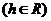 ,则
,则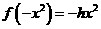 ,而
,而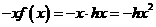 ,∴
,∴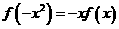 ,即
,即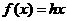 成立。∴
成立。∴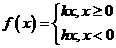 成立。
成立。
(Ⅲ)当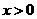 时,
时,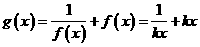 ,
,
令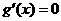 ,得
,得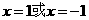 ;
;
当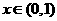 时,
时,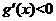 ,∴
,∴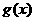 是单调递减函数;
是单调递减函数;
当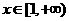 时,
时,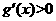 ,∴
,∴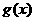 是单调递增函数;
是单调递增函数;
所以当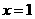 时,函数
时,函数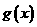 在
在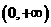 内取得极小值,极小值为
内取得极小值,极小值为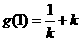
(21)(本大题满分12分)数列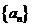 的前
的前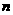 项和为
项和为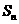 ,已知
,已知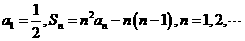
(Ⅰ)写出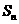 与
与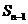 的递推关系式
的递推关系式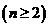 ,并求
,并求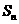 关于
关于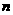 的表达式;
的表达式;
(Ⅱ)设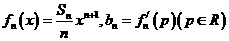 ,求数列
,求数列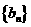 的前
的前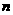 项和
项和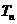 。
。
解:由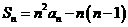
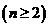 得:
得: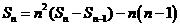 ,即
,即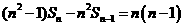 ,所以
,所以 ,对
,对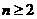 成立。
成立。
由 ,
,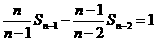 ,…,
,…,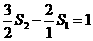 相加得:
相加得: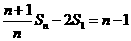 ,又
,又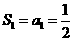 ,所以
,所以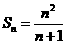 ,当
,当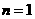 时,也成立。
时,也成立。
(Ⅱ)由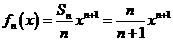 ,得
,得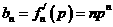 。
。
而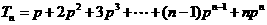 ,
,
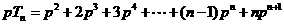 ,
,
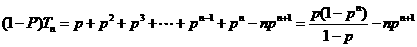
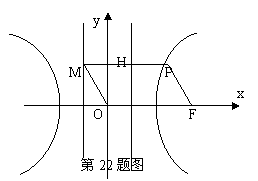
(22)(本大题满分14分)如图,F为双曲线C: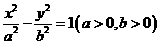 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于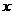 轴上方,M为左准线上一点,
轴上方,M为左准线上一点, 为坐标原点。已知四边形
为坐标原点。已知四边形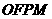 为平行四边形,
为平行四边形,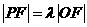 。
。
 (Ⅰ)写出双曲线C的离心率
(Ⅰ)写出双曲线C的离心率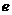 与
与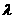 的关系式;
的关系式;
(Ⅱ)当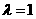 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程。
,求此时的双曲线方程。
解:∵四边形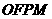 是
是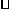 ,∴
,∴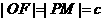 ,作双曲线的右准线交PM于H,则
,作双曲线的右准线交PM于H,则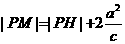 ,又
,又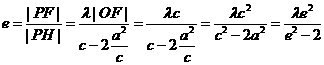 ,
,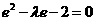 。
。
(Ⅱ)当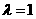 时,
时,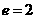 ,
,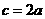 ,
,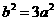 ,双曲线为
,双曲线为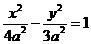 四边形
四边形 是菱形,所以直线OP的斜率为
是菱形,所以直线OP的斜率为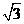 ,则直线AB的方程为
,则直线AB的方程为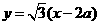 ,代入到双曲线方程得:
,代入到双曲线方程得: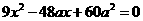 ,
,
又 ,由
,由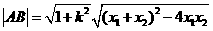 得:
得: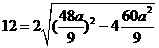 ,解得
,解得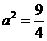 ,则
,则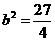 ,所以
,所以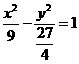 为所求。
为所求。
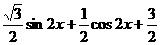
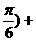
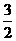 .
∴f(x)的最小正周期T=
.
∴f(x)的最小正周期T=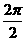 =π.
=π. 由题意得2kπ-
由题意得2kπ-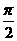 ≤2x+
≤2x+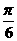 ,k∈Z,
∴f(x)的单调增区间为[kπ-
,k∈Z,
∴f(x)的单调增区间为[kπ-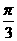 ],k∈Z.
(2)方法一:
先把y=sin 2x图象上所有的点向左平移
],k∈Z.
(2)方法一:
先把y=sin 2x图象上所有的点向左平移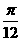 个单位长度,得到y=sin(2x+
个单位长度,得到y=sin(2x+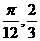 )平移,就得到y=sin(2x+
)平移,就得到y=sin(2x+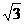 .
而AC=2,
∴AO2+CO2=AC2,
∴∠AOC=90°,即AO⊥OC.
.
而AC=2,
∴AO2+CO2=AC2,
∴∠AOC=90°,即AO⊥OC.
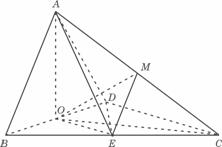

 平面BCD.
平面BCD.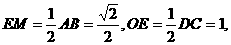
 是直角△AOC斜边AC上的中线,∴
是直角△AOC斜边AC上的中线,∴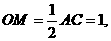
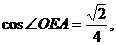
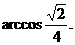
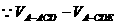 ,
,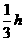 ·S△ACD =
·S△ACD =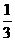 ·AO·S△CDE.
·AO·S△CDE.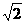 ,
,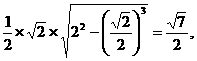
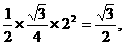
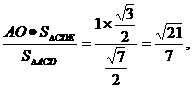
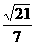 .
.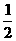 ,
,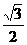 ,0),
,0),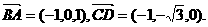
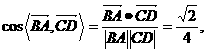
 (Ⅲ)解:设平面ACD的法向量为n=(x,y,z),则
(Ⅲ)解:设平面ACD的法向量为n=(x,y,z),则 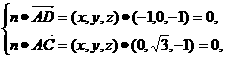
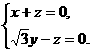
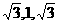 )是平面ACD的一个法向量.
又
)是平面ACD的一个法向量.
又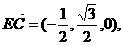
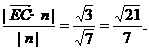
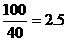 小时,
要耗油(
小时,
要耗油(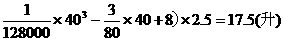 .
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升.
(2)当速度为x千米/小时,汽车从甲地到乙地行驶了
.
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升.
(2)当速度为x千米/小时,汽车从甲地到乙地行驶了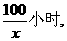 设耗油量为h(x)升,衣题意得
h(x)=(
设耗油量为h(x)升,衣题意得
h(x)=(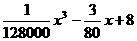 )·
)·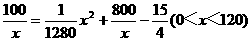 ,
, (0<x≤120=
令h’(x)=0,得x=80.
当x∈(0,80)时,h’(x)<0,h(x)是减函数;
当x∈(80,120)时,h’(x)>0,h(x)是增函数.
∴当x=80时,h(x)取到极小值h(80)=11.25.
因为h(x)在(0,120)上只有一个极值,所以它是最小值.
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
(20)本小题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,
(0<x≤120=
令h’(x)=0,得x=80.
当x∈(0,80)时,h’(x)<0,h(x)是减函数;
当x∈(80,120)时,h’(x)>0,h(x)是增函数.
∴当x=80时,h(x)取到极小值h(80)=11.25.
因为h(x)在(0,120)上只有一个极值,所以它是最小值.
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
(20)本小题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,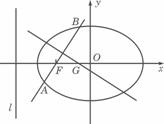

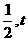 ),则圆半径
),则圆半径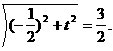 解得t=±
解得t=±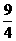 .
(2)设直线AB的方程为y=k(x+1)(k≠0),
代入
.
(2)设直线AB的方程为y=k(x+1)(k≠0),
代入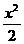 +y2=1,整理得(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),
则x1+x1=-
+y2=1,整理得(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),
则x1+x1=-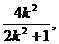
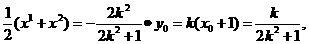

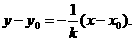
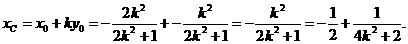
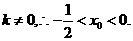
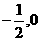 )。
)。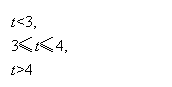 综上,h(t)=
综上,h(t)=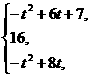
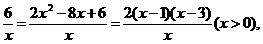
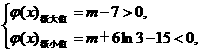 既7<m<-6ln 3.
既7<m<-6ln 3.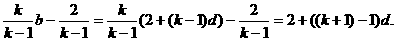
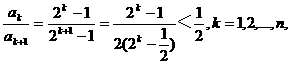
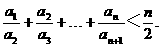
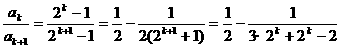 ≥
≥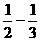 (
(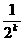 ),k=1,2,…,n,
数 学(文史类)
),k=1,2,…,n,
数 学(文史类)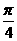 ”的
A.充分而不必要条件
B.必要而不充分条件
”的
A.充分而不必要条件
B.必要而不充分条件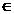 R.
R.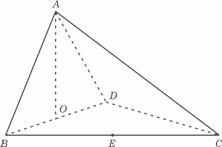
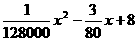 (0<x≤120).已知甲、乙两地相距100千米。
(0<x≤120).已知甲、乙两地相距100千米。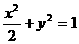 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。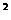 +8x,g(x)=6lnx+m
+8x,g(x)=6lnx+m }满足a
}满足a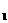 =1,a
=1,a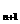 =2a
=2a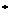 )
)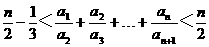 (n∈N*).
数学试题(理工农医类)参考答案
一、选择题:本大题考查基本概念和基本运算,每小题5分,满分60分.
(1)D (2)B (3)A (4)C (5)D (6)A
(7)C (8)A (9)B (10)C (11)B (12)B
二、填空题:本大题考查基础知识和基本运算.每小题4分,满分16分.
(13)10
(14)
(n∈N*).
数学试题(理工农医类)参考答案
一、选择题:本大题考查基本概念和基本运算,每小题5分,满分60分.
(1)D (2)B (3)A (4)C (5)D (6)A
(7)C (8)A (9)B (10)C (11)B (12)B
二、填空题:本大题考查基础知识和基本运算.每小题4分,满分16分.
(13)10
(14)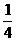 (15)
(15)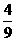 (16)(
(16)(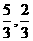 )
)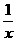 )
)
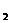 +a
+a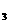 =13,则a
=13,则a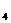 +a
+a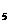 +a
+a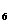 等于
等于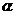 ∈(
∈(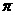 ),sin
),sin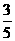 ,则tan(
,则tan(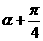 )等于
)等于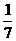 B.7
C.-
B.7
C.- 
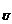 A)∩等于
A)∩等于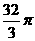 ,那么正方体的棱长等于
,那么正方体的棱长等于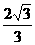 C.
C.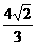 D.
D.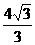
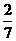 B.
B.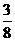 C.
C.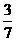 D.
D.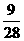
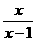 (x﹥1)的反函数是
(x﹥1)的反函数是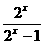 (x>0)
B.y=
(x>0)
B.y= 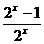 (x>0) D. .y=
(x>0) D. .y= x(
x(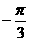 ,
,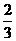 B.
B.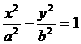 (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ︱=1,︱
︱=1,︱ ︱=
︱=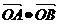 =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设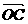 =m
=m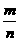 等于
等于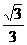 D.
D.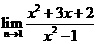 的值等于
的值等于 .
(10)在
.
(10)在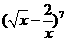 的展开式中,
的展开式中, 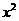 的系数是
的系数是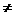 0)共线,则,
0)共线,则, 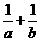 的值等于
的值等于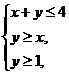 点O为坐标原点,那么|PO |的最小值
点O为坐标原点,那么|PO |的最小值 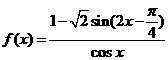 .
. 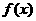 的定义域;
的定义域; 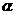 的第四象限的角,且
的第四象限的角,且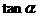
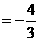 ,求
,求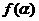 的值
的值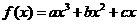 在点
在点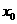 处取得极大值5,其导函数
处取得极大值5,其导函数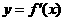
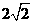 ,记动点 P的轨
,记动点 P的轨 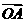 、
、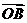 的最小值.
的最小值.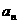 中,若 a1,a2 是正整数,且
中,若 a1,a2 是正整数,且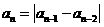 ,
,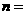 3,4,5,…,则称
3,4,5,…,则称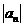
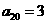 ,
,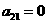 ,数列
,数列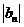 满足
满足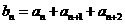
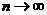 时,
时, 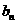 的极限是否存在,如果存在,求出其极
的极限是否存在,如果存在,求出其极 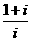 对应的点位于
对应的点位于 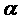 的斜线 AB 交
的斜线 AB 交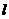 与 AB 垂直,且交
与 AB 垂直,且交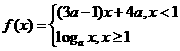 是
是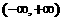 上的增函数,那么 a 的取值范
上的增函数,那么 a 的取值范 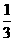 )
) 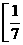 ,
,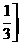 (D)
(D)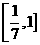
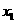 ,
,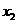 (
(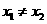 ).
). 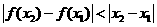 恒成立”的只有
恒成立”的只有 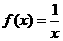 (B)
(B)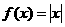
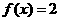 (D)
(D)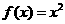
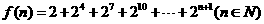 ,则
,则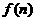 等于
等于 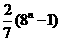 (B)
(B)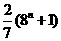
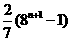 (D)
(D)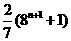
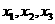 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段 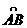 ,
,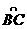
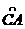 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A)
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A) 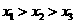
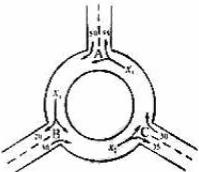 (B)
(B) 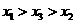

(D)
(D)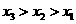
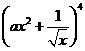 展开式中
展开式中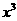 的系数为
的系数为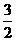 ,则
,则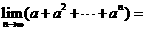 _____。
_____。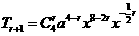 ,由
,由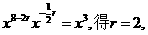
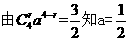 ,所以
,所以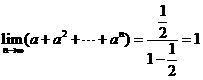 ,所以为1。
,所以为1。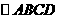 中,
中,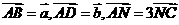 ,M为BC的中点,则
,M为BC的中点,则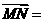 _______。(用
_______。(用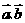 表示)
表示)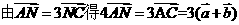 ,
,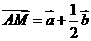 ,所以
,所以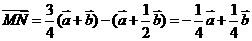 。
。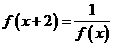 ,若
,若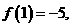 则
则 __________。
__________。 解:由
解:由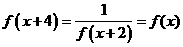 ,所以
,所以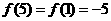 ,则
,则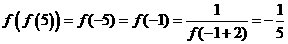 。
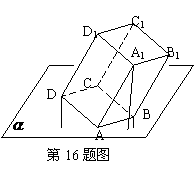
。 内,其余顶点在
内,其余顶点在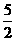 ,所以B1到平面
,所以B1到平面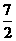 ,所以C1到平面
,所以C1到平面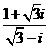 等于( )
等于( )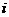 B.
B.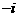 C.
C.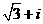 D.
D.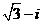
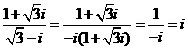 故选A
故选A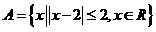 ,
,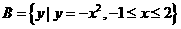 ,则
,则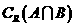 等于( )
等于( )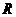 B.
B.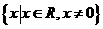 C.
C.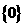 D.
D.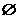
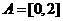 ,
,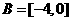 ,所以
,所以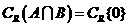 ,故选B。
,故选B。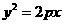 的焦点与椭圆
的焦点与椭圆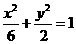 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )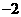 B.
B.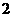 C.
C.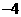 D.
D.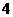
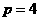 ,故选D。
,故选D。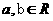 ,已知命题
,已知命题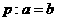 ;命题
;命题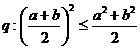 ,则
,则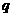 成立的( )
成立的( )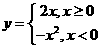 的反函数是( )
的反函数是( )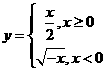 B.
B. C.
C.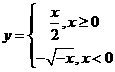 D.
D.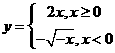
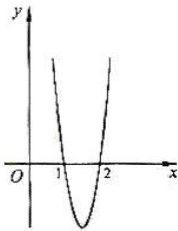
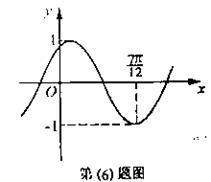 (6)将函数
(6)将函数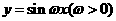 的图象按向量
的图象按向量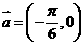 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )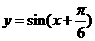 B.
B.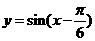
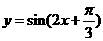 D.
D.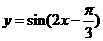
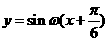 ,由图象知,
,由图象知,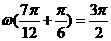 ,所以
,所以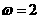 ,因此选C。
,因此选C。 的一条切线
的一条切线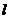 与直线
与直线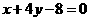 垂直,则
垂直,则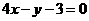 B.
B.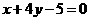 C.
C.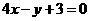 D.
D.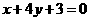
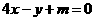 ,即
,即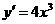 ,所以
,所以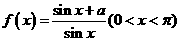 ,下列结论正确的是( )
,下列结论正确的是( )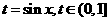 ,则函数
,则函数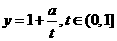 的值域,又
的值域,又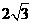 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为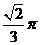 B.
B.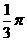 C.
C.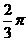 D.
D.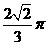
 的正三角形,所以由
的正三角形,所以由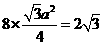 知,
知,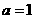 ,则此球的直径为
,则此球的直径为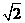 ,故选A。
,故选A。 满足条件
满足条件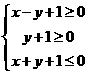 ,那么
,那么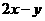 的最大值为( )
的最大值为( ) C.
C.
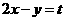 过点(0,-1)时,
过点(0,-1)时,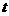 最大,故选B。
最大,故选B。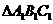 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于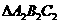 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )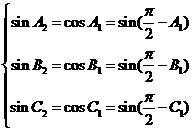 ,得
,得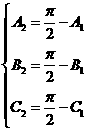 ,那么,
,那么,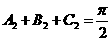 ,所以
,所以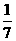 B.
B.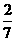 C.
C.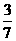 D.
D.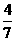
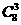 个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得
个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得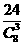 ,所以选C。
,所以选C。
 其中
其中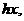
 如图,F为双曲线C:
如图,F为双曲线C:
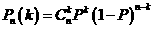
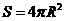 ,其中R表示球的半径
,其中R表示球的半径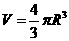 ,其中R表示球的半径
,其中R表示球的半径