|
已知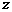 是复数,
是复数,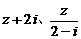 均为实数(
均为实数(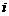 为虚数单位),且复数
为虚数单位),且复数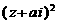 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数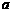 的取值范围.
的取值范围.
[解]
|
已知 是方程
是方程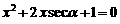 的两个根中较小的根,求
的两个根中较小的根,求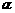 的值.
的值.
[解]
|
第2小题满分8分.
已知正三棱锥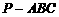 的体积为
的体积为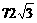 ,侧面与底面所成的二面角的大小为
,侧面与底面所成的二面角的大小为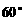 .
.
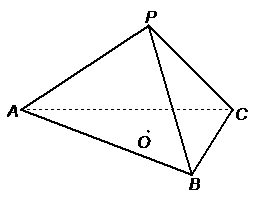 (1)证明:
(1)证明: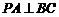 ;
;
(2)求底面中心 到侧面的距离.
到侧面的距离.
[证明](1)
[解](2)
|
第2小题满分8分.
某市2004年底有住房面积1200万平方米,计划从2005年起,每年拆除20万平方米的旧住房. 假定该市每年新建住房面积是上年年底住房面积的5%.
(1)分别求2005年底和2006年底的住房面积 ;
(2)求2024年底的住房面积.(计算结果以万平方米为单位,且精确到0.01)
[解](1)
(2)
|
第2小题满分6分,第3小题满分7分.
 已知函数
已知函数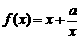 的定义域为
的定义域为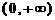 ,且
,且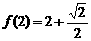 . 设点
. 设点 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点 分别作直线
分别作直线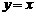 和
和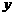 轴的垂线,垂足分别为
轴的垂线,垂足分别为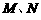 .
.
(1)求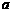 的值;
的值;
(2)问: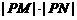 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设 为坐标原点,求四边形
为坐标原点,求四边形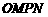 面积的最小值.
面积的最小值.
[解](1)
(2)
(3)
|
第2小题满分8分. 第3小题满分5分.
(1)求右焦点坐标是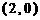 ,且经过点
,且经过点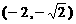 的椭圆的标准方程;
的椭圆的标准方程;
(2)已知椭圆 的方程是
的方程是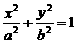
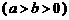 . 设斜率为
. 设斜率为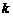 的直线
的直线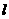 ,交椭圆
,交椭圆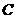 于
于
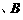 两点,
两点, 的中点为
的中点为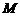 . 证明:当直线
. 证明:当直线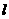 平行移动时,动点
平行移动时,动点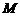 在一条过原点的定直线上;
在一条过原点的定直线上;
(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
 [解](1)
[解](1)
[证明](2)
[解](3)
普通高等学校春季招生考试
12. 已知函数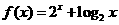 ,数列
,数列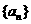 的通项公式是
的通项公式是 (
(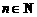 ),当
),当
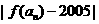 取得最小值时,
取得最小值时,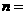 .
.
|
四个结论,其中有且只有一个结论是正确的,必须把正确结论的
代号写在题后的圆括号内,选对得 4分,否则一律得零分.
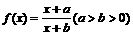 ,求
,求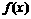 的单调区间,并证明
的单调区间,并证明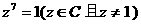 .
.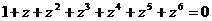 ;
;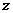 的辐角为
的辐角为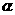 ,求
,求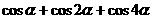 的值.
的值.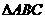 所在平面的一条斜线,点N是V在平面ABC上的射影,且在
所在平面的一条斜线,点N是V在平面ABC上的射影,且在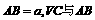 之间的距离为
之间的距离为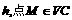 .
.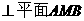 ;
;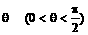 ,求四面体MABC的体积.
,求四面体MABC的体积.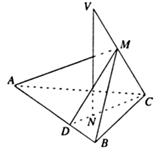
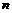 个正数
个正数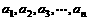 ,使这
,使这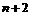 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入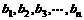 ,使这
,使这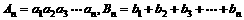 .
.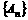 和
和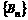 的通项;
的通项;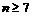 时,比较
时,比较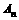 与
与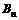 的大小,并证明你的结论.
的大小,并证明你的结论.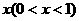 ,则出厂价相应提高的比例为0.75
,则出厂价相应提高的比例为0.75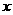 ,同时预计年销售量增加的比例为0.6
,同时预计年销售量增加的比例为0.6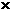 年销售量.
年销售量.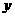 与投入成本增加的比例
与投入成本增加的比例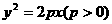 .过动点M(
.过动点M(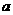 ,0)且斜率为1的直线
,0)且斜率为1的直线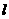 与该抛物线交于不同的两点A、B,
与该抛物线交于不同的两点A、B,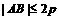 .
.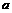 的取值范围;
的取值范围;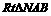 面积的最大值.
面积的最大值.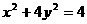 长轴上一个顶点为A,以A为直角顶点作一个内接于椭圆的等腰直角三角形,该三角形的面积是_______________.
长轴上一个顶点为A,以A为直角顶点作一个内接于椭圆的等腰直角三角形,该三角形的面积是_______________.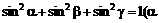 、
、 、
、 均为锐角),那么
均为锐角),那么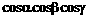 的最大值等于____________________.
的最大值等于____________________. 、
、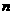 是直线,
是直线,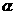 、
、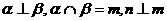 ,则
,则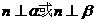 ;
; ,则
,则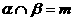 ,
,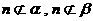 ,则
,则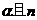 ∥
∥ 的子集个数是
的子集个数是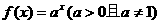 对于任意的实数
对于任意的实数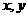 都有
都有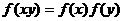 (B)
(B)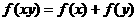
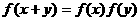 (D)
(D)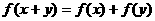
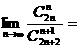
 (D)
(D)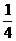
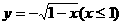 的反函数是
的反函数是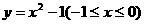 (B)
(B)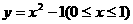
 (D)
(D)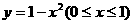
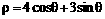 的圆心的坐标是
的圆心的坐标是 (B)
(B) (C)
(C) (D)
(D)
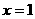 上,O为坐标原点.以OP为直角边、点O为直角顶点作等腰
上,O为坐标原点.以OP为直角边、点O为直角顶点作等腰 ,则动点Q的轨迹是
,则动点Q的轨迹是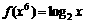 ,那么
,那么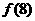 等于
等于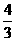 (B)8 (C)18 (D)
(B)8 (C)18 (D)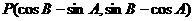 在
在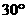 (B)
(B)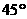 (C)
(C) (D)
(D)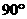
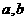 满足
满足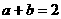 ,则
,则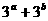 的最小值是
的最小值是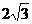 (D)
(D)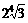
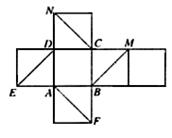 ①
①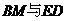 平行
平行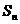 (万件)近似地满足
(万件)近似地满足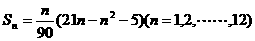
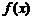 的定义域为
的定义域为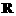 ,有下列三个命题:
,有下列三个命题: ,有
,有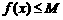 ,则
,则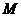 是函数
是函数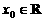 ,使得对任意
,使得对任意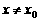 ,有
,有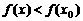 ,则
,则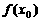 是函数
是函数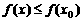 ,则
,则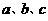 是常数,则“
是常数,则“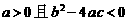 ”是“对任意
”是“对任意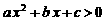 ”
”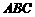 中,若
中,若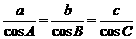 ,则△
,则△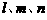 及平面
及平面 ,下列命题中的假命题是
,下列命题中的假命题是 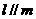 ,
,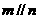 ,则
,则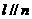 . (B)若
. (B)若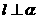 ,
,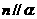 ,则
,则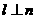 .
.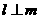 ,
,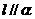 ,
,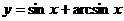 的值域是
.
的值域是
.