摘要:已知函数f(x)=sin2x+xcosx+2cos2x,xR. (I)求函数f(x)的最小正周期和单调增区间, (Ⅱ)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到? 如图.四面体ABCD中.O.E分别BD.BC的中点,CA=CB=CD=BD=2 (Ⅰ)求证:AO⊥平面BCD, (Ⅱ)求异面直线AB与CD所成角的大小, (Ⅲ)求点E到平面的距离. 统计表明.某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x的函数解析式可以表示为:y=(0<x≤120).已知甲.乙两地相距100千米. (Ⅰ)当汽车以40千米/小时的速度匀速行驶时.从甲地到乙地要耗油多少升? (Ⅱ)当汽车以多大的速度匀速行驶时.从甲地到乙地耗油最少?最少为多少升? 已知椭圆的左焦点为F.O为坐标原点. (Ⅰ)求过点O.F.并且与椭圆的左准线l相切的圆的方程, (Ⅱ)设过点F且不与坐标轴垂直交椭圆于A.B两点.线段AB的垂直平分线与x轴交于点G.求点G横坐标的取值范围. 已知函数f(x)=-x+8x,g(x)=6lnx+m (Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t); (Ⅱ)是否存在实数m.使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在.求出m的取值范围,.若不存在.说明理由. 已知数列{a}满足a=1,a=2a+1(n∈N) (Ⅰ)求数列{a}的通项公式, (Ⅱ)若数列{bn}满足4k1-14k2-1-4k-1=(an+1)km(n∈N*),证明:{bn}是等差数列; (Ⅲ)证明:(n∈N*). 数学试题参考答案 一.选择题:本大题考查基本概念和基本运算.每小题5分.满分60分. A A B B 二.填空题:本大题考查基础知识和基本运算.每小题4分.满分16分. (15) (16)()
网址:http://m.1010jiajiao.com/timu3_id_4468819[举报]
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当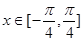 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
查看习题详情和答案>>
((本小题满分12分)
编号分别为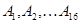 的16名篮球运动员在某次比赛中得分记录如下;
的16名篮球运动员在某次比赛中得分记录如下;
|
编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
|
得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
|
编号 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
|
得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间的人数填入相应的空格内:
|
区 间 |
|
|
|
|
人 数 |
|
|
|
(Ⅱ)从得分在区间 内的运动员中随机抽取2人.
内的运动员中随机抽取2人.
(1)用运动员编号列出所有可能的抽取结果;
(2)求这两人得分之和大于50的概率.
查看习题详情和答案>>
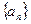 中,
中,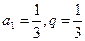 ,
,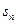 为数列
为数列 项的和,证明:
项的和,证明:
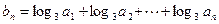 ,求数列
,求数列 的通项公式;
的通项公式;