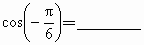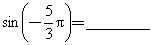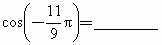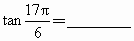摘要:案填在题中横线上. (9)的值等于. (10)在的展开式中, 的系数是. .B(ab0)共线.则, 的值等于 (12)在△ABC 中.若 C B A sin A: sinB: sinC =5:7:8. 则∠B 的大小是 的坐标满足条件点O为坐标原点.那么|PO |的最小值 等于,最大值等于. (14)已知A.B.C三点在球心为 O.半径为R 的球面上.AC⊥BC.且 AB=R.那么 A.B 两点间的球面距离为 球心到平面 ABC 的距离为. . 三.解答题:本大题共 6 小题.共 80 分.解答应写出文字说明.证明过程或演算步骤. 已知函数. (Ⅰ)求的定义域, (Ⅱ)设的第四象限的角.且.求的值 已知函数在点处取得极大值5.其导函数 的图象经过点.如图所示.求: (Ⅰ)的值, (Ⅱ)a.b.c 的值. 如图.在底面为平行四边形的四棱锥 P-ABCD 中.AB⊥AC.PA⊥平面 ABCD.且 PA=PB.点 E 是 PD 的中点. (Ⅰ)求证:AC⊥PB, (Ⅱ)求证:PB//平面 AEC, (Ⅲ)求二面角 E-AC-B 的大小. 某公司招聘员工.指定三门考试课程.有两种考试方案. 方案一:考试三门课程.至少有两门及格为考试通过, 方案二:在三门课程中.随机选取两门.这两门都及格为考试通过. 假设某应聘者对三门指定课程考试及格的概率分别是 a.b.c.且三门课程考 试是否及格相互之间没有影响. 求: (Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率, (Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小. 已知点 M.动点 P满足条件|PM |-|PN |=.记动点 P的轨 迹为 W. (Ⅰ)求 W 的方程, (Ⅱ)若 A.B 是W上的不同两点.O 是坐标原点.求 .的最小值. 在数列中.若 a1.a2 是正整数.且,3.4.5.-.则称 为“绝对差数列 . (Ⅰ)举出一个前五项不为零的“绝对差数列 , (Ⅱ)若“绝对差数列 中.,.数列满足 n=1.2.3.-.分虽判断当时, 与的极限是否存在.如果存在.求出其极 限值, (Ⅲ)证明:任何“绝对差数列 中总含有无穷多个为零的项.
网址:http://m.1010jiajiao.com/timu3_id_4468816[举报]
将下列三角函数转化为锐角三角函数,并填在题中横线上:
|
(1)cos210° =________; |
(2)sin263°42′ =________; |
|
(3) |
(4) |
|
(5) |
(6)cos( -104°26′)=________; |
|
(7)tan632°24′ =________; |
(8) |
等差数列![]() 中,
中,![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 的值为
的值为
A、18 B、16 C、15 D、14
第Ⅱ卷(非选择题 共90分)
二. 填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
查看习题详情和答案>>
某班一次期中考试之后,从全班同学中随机抽出5位,这5位同学的数学、物理分数见下表:先完成下面(1)~(2)的统计分析,将结果直接写在题中横线上,然后解答第(3)小题.
(1)研究变量y与x的相关关系时,计算得r≈0.94,这说明y与x的相关程度是 .
(2)求得y与x的线性回归方程之后,该方程所表示的直线一定过点 .
(3)求y与x的线性回归方程,并估计该班本次考试数学成绩为60分的学生的物理成绩. 查看习题详情和答案>>
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 数学分数x | 70 | 75 | 80 | 85 | 90 |
| 物理分数y | 73 | 77 | 80 | 88 | 86 |
(2)求得y与x的线性回归方程之后,该方程所表示的直线一定过点
(3)求y与x的线性回归方程,并估计该班本次考试数学成绩为60分的学生的物理成绩. 查看习题详情和答案>>