0 446772 446780 446786 446790 446796 446798 446802 446808 446810 446816 446822 446826 446828 446832 446838 446840 446846 446850 446852 446856 446858 446862 446864 446866 446867 446868 446870 446871 446872 446874 446876 446880 446882 446886 446888 446892 446898 446900 446906 446910 446912 446916 446922 446928 446930 446936 446940 446942 446948 446952 446958 446966 447348
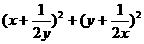 的最小值是 ( )
的最小值是 ( )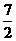 C.4 D.
C.4 D.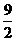
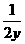 )(y+
)(y+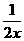 )≥8
)≥8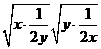 =4当且仅当
=4当且仅当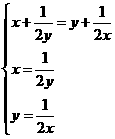 ,得x=y=
,得x=y=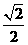 时等号成立,选(C)
时等号成立,选(C)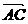 与
与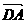 的夹角为 ( )
的夹角为 ( )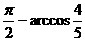 B.
B.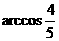 C.
C.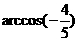 D.-
D.-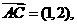 D(5,2),
D(5,2),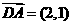 ,
,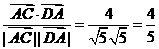 ,∴∴∠DAC=
,∴∴∠DAC=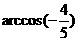 ,即向量
,即向量 是定义在R上的偶函数,在
是定义在R上的偶函数,在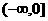 上是减函数,且
上是减函数,且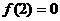 ,则使得
,则使得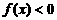 的x的取值范围是 ( )
的x的取值范围是 ( )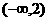 B.
B.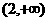 C.
C.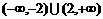 D.(-2,2)
D.(-2,2)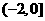 ,又由对称性
,又由对称性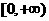 ,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)
,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)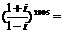 ( )
( )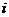 B.-
B.- D.-
D.-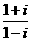 =-i,∴
=-i,∴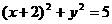 关于原点(0,0)对称的圆的方程为 ( )
关于原点(0,0)对称的圆的方程为 ( )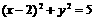 B.
B.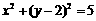
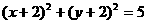 D.
D.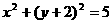
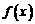 和
和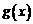 的图象关于原点对称,且
的图象关于原点对称,且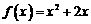 .
.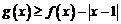 ;
;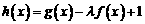 在
在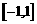 上是增函数,求实数
上是增函数,求实数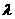 的取值范围.
的取值范围.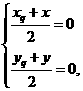 即
即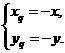 ∵点Qxq,yq)在函数f(x)的图象上,
∵点Qxq,yq)在函数f(x)的图象上,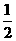 ,因此,原不等式的解集为[-1,
,因此,原不等式的解集为[-1,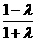 .
.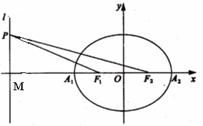 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.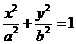 (a>0,b>0),半焦距为c,则|MA1|=
(a>0,b>0),半焦距为c,则|MA1|=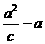 ,|A1F1|=a-c
由题意,得
,|A1F1|=a-c
由题意,得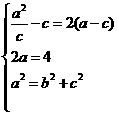 ∴a=2,b=
∴a=2,b=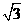 ,c=1.
,c=1.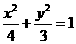
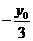 ,直线PF2的斜率k2=
,直线PF2的斜率k2=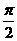 ,∴∠F1PF2为锐角.
,∴∠F1PF2为锐角.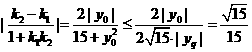
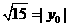 ,即|y0|=
,即|y0|=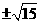 时,tan∠F1PF2取到最大值此时∠F1PF2最大,∴
时,tan∠F1PF2取到最大值此时∠F1PF2最大,∴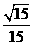 .
.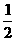 PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.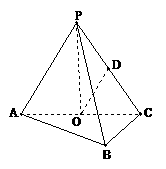
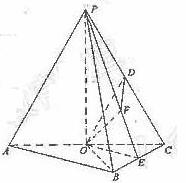
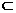 平面PAB,∴OD∥平面PAB.
平面PAB,∴OD∥平面PAB.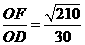 ,∴PA与平面PBC所成角为arcsin
,∴PA与平面PBC所成角为arcsin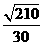
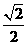 a,0,0).
a,0,0).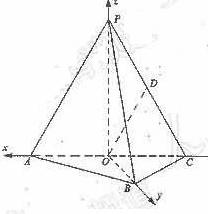
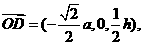 又
又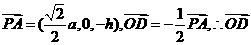 ∥
∥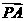 ,
,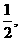 则PA=2a,∴h=
则PA=2a,∴h=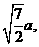 ∴
∴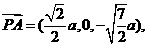 可求得平面PBC的法向量
可求得平面PBC的法向量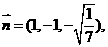
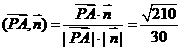 .
.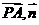 )|=
)|=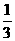 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.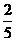 ,求p的值.
,求p的值. 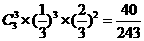
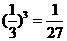
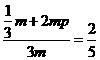 ,得p=
,得p=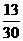 .
.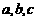 成等差数列,
成等差数列,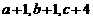 成等比数列,且
成等比数列,且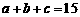 ,求
,求