摘要：19．如图.已知椭圆的中心在坐标原点.焦点F1.F2在x轴上.长轴A1A2的长为4.左准线l与x轴的交点为M.|MA1|∶|A1F1|＝2∶1． (Ⅰ)求椭圆的方程, (Ⅱ)若点P为l上的动点.求∠F1PF2最大值． 解:(Ⅰ)设椭圆的方程为,半焦距为c,则|MA1|=,|A1F1|=a-c 由题意,得∴a=2,b=,c=1. 故椭圆的方程为 (Ⅱ)设P(-4,y0),y0≠0, ∴只需求tan∠F1PF2的最大值即可. 设直线PF1的斜率k1=,直线PF2的斜率k2=, ∵0<∠F1PF2<∠PF1M<,∴∠F1PF2为锐角. ∴tan∠F1PF2= 当且仅当,即|y0|=时,tan∠F1PF2取到最大值此时∠F1PF2最大,∴ ∠F1PF2的最大值为arctan.
网址：http://m.1010jiajiao.com/timu3_id_4468694[举报]
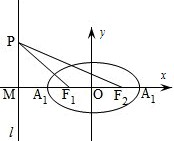如图，已知椭圆的中心在坐标原点，焦点F1，F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，|MA1|：|A1F1|=2：1．（Ⅰ）求椭圆的方程；
（Ⅱ）若点P在直线l上运动，求∠F1PF2的最大值、 查看习题详情和答案>>
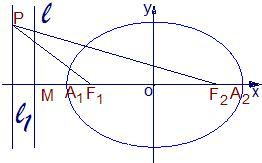如图，已知椭圆的中心在坐标原点，焦点F1，F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，|MA1|：|A1F1|=2：1．（Ⅰ）求椭圆的方程；
（Ⅱ）若直线l1：x=m（|m|＞1），P为l1上的动点，使∠F1PF2最大的点P记为Q，求点Q的坐标（用m表示）． 查看习题详情和答案>>
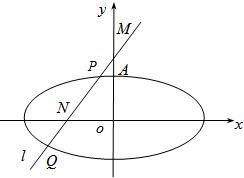如图，已知椭圆的中心在坐标原点，焦点在x轴上，它的一个顶点为A（0，| 2 |
| ||
| 2 |
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设
|
| ||
|
|
|
| ||
|
|
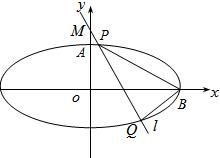如图，已知椭圆的中心在坐标原点，焦点在x轴上，它的一个顶点为A（0，
如图，已知椭圆的中心在坐标原点，焦点在x轴上，它的一个顶点为A（0，