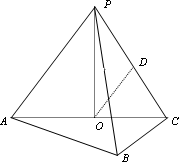
摘要:18.如图.在三棱锥P-ABC中.AB⊥BC.AB=BC=PA.点O.D分别是AC.PC的中点.OP⊥底面ABC. (Ⅰ)求证:OD∥平面PAB, (Ⅱ) 求直线OD与平面PBC所成角的大小. 解:解法一 (Ⅰ)∵O.D分别为AC.PC的中点:∴OD∥PA,又AC平面PAB,∴OD∥平面PAB. (Ⅱ)∵AB⊥BC,OA=OC,∴OA=OC=OB,又∵OP⊥平面ABC,∴PA=PB=PC. 取BC中点E,连结PE,则BC⊥平面POE,作OF⊥PE于F,连结DF,则OF⊥平面PBC ∴∠ODF是OD与平面PBC所成的角. 又OD∥PA,∴PA与平面PBC所成角的大小等于∠ODF. 在Rt△ODF中,sin∠ODF=,∴PA与平面PBC所成角为arcsin 解法二: ∵OP⊥平面ABC,OA=OC,AB=BC,∴OA⊥OB,OA⊥OP,OB⊥OP. 以O为原点,射线OP为非负x轴,建立空间坐标系O-xyz如图),设AB=a,则A(a,0,0). B(0, a,0),C(-a,0,0).设OP=h,则P. (Ⅰ)∵D为PC的中点,∴又∥, ∴OD∥平面PAB. (Ⅱ)∵k=则PA=2a,∴h=∴可求得平面PBC的法向量 ∴cos. 设PA与平面PBC所成角为θ,刚sinθ=|cos()|=. ∴PA与平面PBC所成的角为arcsin.
网址:http://m.1010jiajiao.com/timu3_id_4468693[举报]
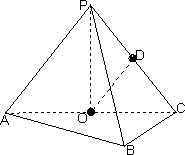
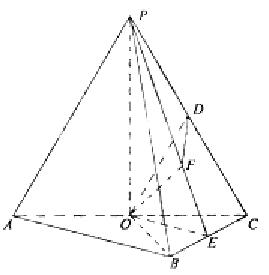
18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证OD∥平面PAB;
(Ⅱ)当k=![]() 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
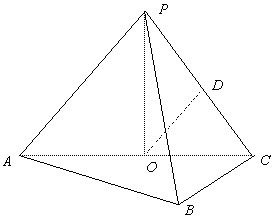
18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=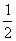 PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证:OD∥平面PAB;
(Ⅱ)求直线OD与平面PBC所成角的大小.
| |||||||||||