(15)(本小题满分13分)
已知向量 m = (cos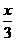 ,
,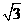 cos
cos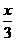 ),n = (sin
),n = (sin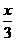 ,cos
,cos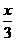 ),函数f(x) = m·n .
),函数f(x) = m·n .
(Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
(17)(本小题满分13分)
某大学的研究生入学考试有50人参加,其中英语与政治成绩采用5分制,设政治成绩为x,英语成绩为y,结果如下表:
 y 人数
y 人数x |
英
语 |
|||||
|
1分 |
2分 |
3分 |
4分 |
5分 |
||
|
政
治 |
1分 |
1 |
3 |
1 |
0 |
1 |
|
2分 |
1 |
0 |
7 |
5 |
1 |
|
|
3分 |
2 |
1 |
0 |
9 |
3 |
|
|
4分 |
1 |
b |
6 |
0 |
a |
|
|
5分 |
0 |
0 |
1 |
1 |
3 |
(Ⅰ)求a +b的值;
(Ⅱ)求政治成绩为4分且英语成绩为3分的概率;
(Ⅲ)若“考生的政治成绩为4分” 与“英语成绩为2分”是相互独立事件,求a、b的值;
(Ⅳ)若y的数学期望为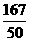 ,求a、b的值.
,求a、b的值.
(18)(本小题满分13分)
如图,已知圆C: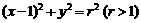 ,设M为圆C与x轴负
,设M为圆C与x轴负
半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
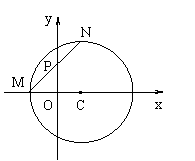 (Ⅰ)当r=2时, 求满足条件的P点的坐标;
(Ⅰ)当r=2时, 求满足条件的P点的坐标;
 (Ⅱ)当r∈(1,+∞)时,求点N的轨迹G的方程;
(Ⅱ)当r∈(1,+∞)时,求点N的轨迹G的方程;
(Ⅲ)过点P(0,2)的直线l与(Ⅱ)中轨迹G相交于两个不同
的点E、F,若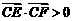 ,求直线
,求直线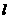 的斜率的取值范围.
的斜率的取值范围.
(19)(本小题满分14分)
设对于任意实数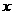 、
、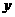 ,函数
,函数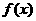 、
、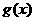 满足
满足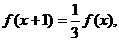 且
且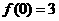 ,
,
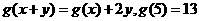 ,
,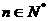 .
.
(Ι)求数列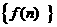 、
、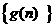 的通项公式;
的通项公式;
(ΙΙ)设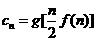 ,求数列
,求数列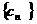 的前
的前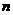 项和Sn;
项和Sn;
(ΙΙΙ)已知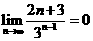 ,设
,设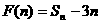 ,是否存在整数
,是否存在整数 和
和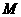 ,使得对任意正整数
,使得对任意正整数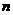 不等式
不等式 <
<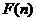 <
<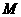 恒成立?若存在,分别求出
恒成立?若存在,分别求出 和
和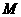 的集合,并求出
的集合,并求出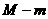 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
(20)(本小题满分14分)
已知函数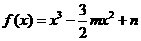 ,
,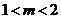
(Ⅰ)若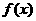 在区间
在区间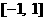 上的最大值为1,最小值为
上的最大值为1,最小值为 ,求
,求 、
、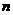 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求经过点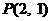 且与曲线
且与曲线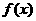 相切的直线
相切的直线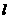 的方程;
的方程;
(Ⅲ)设函数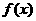 的导函数为
的导函数为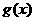 ,函数
,函数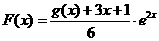 ,试判断函数
,试判断函数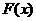 的极值点个数,并求出相应实数
的极值点个数,并求出相应实数 的范围.
的范围.
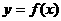 的反函数
的反函数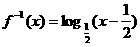 ,则方程
,则方程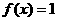 的解是 .
的解是 . 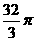 ,那么这个球的半径是 ,三棱柱的体积是
.
,那么这个球的半径是 ,三棱柱的体积是
.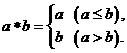 则对x∈R,函数f(x)=1*x的解析式为f(x)= .
则对x∈R,函数f(x)=1*x的解析式为f(x)= .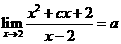 ,则c =
, a= .
,则c =
, a= .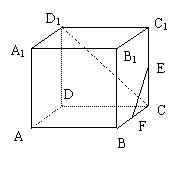 (3) 正方体ABCD-A1B1C1D1中,E、F分别是棱C1C与
(3) 正方体ABCD-A1B1C1D1中,E、F分别是棱C1C与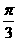 )的图像,只需将函数y=2sin2x的图像 ( )
)的图像,只需将函数y=2sin2x的图像 ( )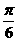 个单位 (D)
向右平移
个单位 (D)
向右平移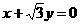 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转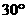 ,所得直线与圆
,所得直线与圆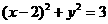 的位置关系是
( )
的位置关系是
( )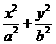 =1 (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且
=1 (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且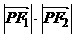 的最大值的取值范围是[2c2,3c2],其中
的最大值的取值范围是[2c2,3c2],其中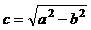 . 则椭圆M的离心率e的取值范围是
( )
. 则椭圆M的离心率e的取值范围是
( )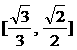 (B)
(B)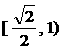 (C)
(C)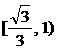 (D)
(D)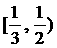
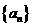 中,
中,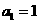 ,
,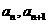 是方程
是方程 的两个根,则数列
的两个根,则数列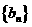 的前
的前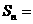 ( )
( )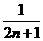 (B)
(B)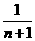 (C)
(C) 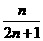 (D)
(D)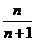
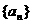 是等差数列,
是等差数列,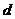 为公差且不为0,
为公差且不为0,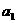 和
和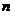 项和记作
项和记作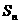 ,设集合
,设集合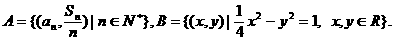
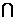 B至多有一个元素;
B至多有一个元素;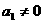 时,一定有A
时,一定有A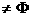 。
。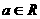 ,二次函数
,二次函数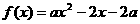 。设不等式
。设不等式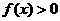 的解集为A,又知集合B=
的解集为A,又知集合B=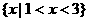 。若
。若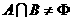 ,求
,求 的取值范围。
的取值范围。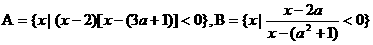 。
。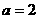 时,求
时,求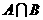 ;
;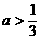 时,求使
时,求使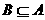 的实数
的实数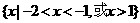 ,集合B=
,集合B=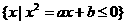 。已知
。已知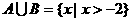 ,
,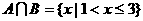 。试求
。试求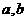 的值。
的值。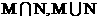 ;
;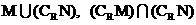 。
。 满足:(1)对任意
满足:(1)对任意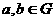 ,都有
,都有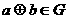 ;(2)存在
;(2)存在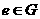 ,使得对一切
,使得对一切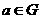 ,都有
,都有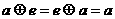 ,则称G关于运算
,则称G关于运算