0 138015 138023 138029 138033 138039 138041 138045 138051 138053 138059 138065 138069 138071 138075 138081 138083 138089 138093 138095 138099 138101 138105 138107 138109 138110 138111 138113 138114 138115 138117 138119 138123 138125 138129 138131 138135 138141 138143 138149 138153 138155 138159 138165 138171 138173 138179 138183 138185 138191 138195 138201 138209 447348
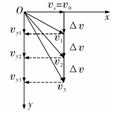 水平方向分速度保持vx=v0,竖直方向,加速度恒为g,速度vy=gt,从抛出点看,每隔Δt时间的速度的矢量关系如图所示.这一矢量关系有两个特点:
水平方向分速度保持vx=v0,竖直方向,加速度恒为g,速度vy=gt,从抛出点看,每隔Δt时间的速度的矢量关系如图所示.这一矢量关系有两个特点: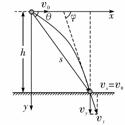 速度、位移:
速度、位移: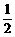 gt2
gt2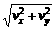
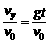
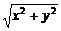
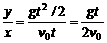
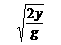 (t由下落高度y决定).
(t由下落高度y决定).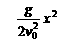 (在未知时间情况下应用方便).
(在未知时间情况下应用方便).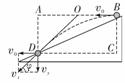 b.连续相等时间内竖直位移之差为Δy=gt2
b.连续相等时间内竖直位移之差为Δy=gt2 [例3]如图所示,卡车通过定滑轮牵引河中的小船,小船一直沿水面运动.在某一时刻卡车的速度为v,绳AO段与水平面夹角为θ,不计摩擦和轮的质量,则此时小船的水平速度多大?
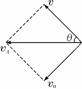
[例3]如图所示,卡车通过定滑轮牵引河中的小船,小船一直沿水面运动.在某一时刻卡车的速度为v,绳AO段与水平面夹角为θ,不计摩擦和轮的质量,则此时小船的水平速度多大?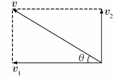 [错解]将绳的速度按右图所示的方法分解,则v1即为船的水平速度
[错解]将绳的速度按右图所示的方法分解,则v1即为船的水平速度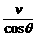
 [正解]小船的运动为平动,而绳AO上各点的运动是平动加转动.以连接船上的A点为研究对象,如图所示,A的平动速度为v,转动速度为vn,合速度vA即与船的平动速度相同.则由图可以看出vA=
[正解]小船的运动为平动,而绳AO上各点的运动是平动加转动.以连接船上的A点为研究对象,如图所示,A的平动速度为v,转动速度为vn,合速度vA即与船的平动速度相同.则由图可以看出vA=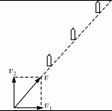 (2)若船在静水中的速度v2=1.5
m/s,要使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
(2)若船在静水中的速度v2=1.5
m/s,要使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?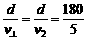 s=36 s
s=36 s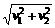 =
=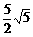 m/s
m/s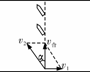 s=v合t=90
s=v合t=90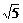 m
m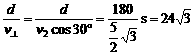 s
s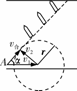 与(1)中②不同,因为船速小于水速,所以船一定向下游漂移,设合速度方向与河岸下游方向夹角为α,则航程s=
与(1)中②不同,因为船速小于水速,所以船一定向下游漂移,设合速度方向与河岸下游方向夹角为α,则航程s=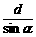 ,欲使航程最短,需α最大,如图所示,由出发点A作出v1矢量,以v1矢量末端为圆心,v2大小为半径作圆,A点与圆周上某点的连线即为合速度方向,欲使v合与水平方向夹角最大,应使v合与圆相切,即v合⊥v2.
,欲使航程最短,需α最大,如图所示,由出发点A作出v1矢量,以v1矢量末端为圆心,v2大小为半径作圆,A点与圆周上某点的连线即为合速度方向,欲使v合与水平方向夹角最大,应使v合与圆相切,即v合⊥v2.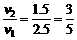
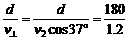 s=150 s
s=150 s [拓展2]在民族运动会上有一个骑射项目,运动员骑在奔驰的马背上,弯弓放箭射击侧向的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭速度为v2,跑道离固定目标的最近距离为d,则( BC )
[拓展2]在民族运动会上有一个骑射项目,运动员骑在奔驰的马背上,弯弓放箭射击侧向的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭速度为v2,跑道离固定目标的最近距离为d,则( BC )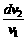
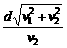
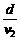
 易错门诊
易错门诊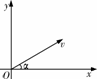 A.因为有Fx,质点一定做曲线运动
A.因为有Fx,质点一定做曲线运动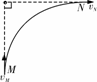 [拓展1]如图所示,一物体在水平恒力作用下沿光滑的水平面做曲线运动,当物体从M点运动到N点时,其速度方向恰好改变了90°,则物体在M点到N点的运动过程中,物体的动能将( C )
[拓展1]如图所示,一物体在水平恒力作用下沿光滑的水平面做曲线运动,当物体从M点运动到N点时,其速度方向恰好改变了90°,则物体在M点到N点的运动过程中,物体的动能将( C ) 典例精析
典例精析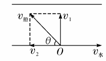 (1)船过河的最短时间
(1)船过河的最短时间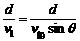 ,可以看出,d、v船一定时,t随sin θ增大而减小.当θ=90°时,即船头与河岸垂直时,过河时间最短tmin=
,可以看出,d、v船一定时,t随sin θ增大而减小.当θ=90°时,即船头与河岸垂直时,过河时间最短tmin=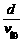 ,到达对岸时船沿水流方向的位移x=v水tmin=
,到达对岸时船沿水流方向的位移x=v水tmin=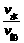 d.
d.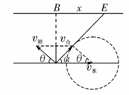 如图所示,无论船向哪一个方向开,船不可能垂直于河岸过河.设船头与河岸成θ角,合速度v合与河岸成α角.可以看出:α角越大,船漂下的距离x越短,那么,在什么条件下α角最大呢?以v水的矢尖为圆心,v船为半径画圆,当v合与圆相切时,α角最大,根据cos θ=
如图所示,无论船向哪一个方向开,船不可能垂直于河岸过河.设船头与河岸成θ角,合速度v合与河岸成α角.可以看出:α角越大,船漂下的距离x越短,那么,在什么条件下α角最大呢?以v水的矢尖为圆心,v船为半径画圆,当v合与圆相切时,α角最大,根据cos θ=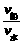 ,船头与河岸的夹角应为θ=arccos
,船头与河岸的夹角应为θ=arccos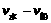 cos θ)
cos θ) 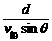 .此情形下船过河的最短位移x=
.此情形下船过河的最短位移x=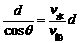 .
.