13．(10分)在近地表面上空，一枚质量为M的火箭，依靠向正下方喷气在空中保持静止，如果喷出气体的速度为v，那么火箭发动机的功率是多少？(火箭的质量视为不变)
解析：如图所示选取在Δt时间内喷出的气体柱Δm为研究对象，设火箭推气体的力为F，根据动量定理有FΔt＝Δmv(忽略了Δm气体本身的重力)因为火箭静止在空中，根据牛顿第三定律有F′＝F＝Mg对这一部分气体，发动机所做的功W等于这部分气体动能的增加，根据动能定理有W＝Δmv2
根据功率的概念有P＝＝＝Mgv.
答案：Mgv
|
图6－11 |
解析：以向右为正方向，列如下动量式：
第一次推球：Mv1＝mv(动量变化量大小相等)
第二次推球：Mv2－Mv1＝2mv
⋮
第n次推球：Mvn－Mvn－1＝2mv
累加得vn＝v
令vn≥v，即n≥×＝＝8.25
即人推9次后不能再接住球．
答案：9
|
图6－12 |
放在小车最左端表面上的小物块．开始时，物块随小车一起以相同的水平速度向左运动，接着物块与挡板发生了第一次碰撞，碰后物块相对于车静止时的位置离小车最左端的距离等于车长的.此后物块又与挡板发生了多次碰撞，最后物块恰未从小车上滑落．若物块与小车表面间的动摩擦因数是个定值，物块与挡板发生碰撞时无机械能损失且碰撞时间极短，试确定小车与物块的质量关系．
解析：设小车初速度为v0，B与车相互作用摩擦力为Ff，小车车长为L，第一次A、B相对静止时速度为v1，由动量守恒，得
mAv0－mBv0＝(mA+mB)v1
由能量守恒，得mAv02+mBv02
＝Ff·L+(mA+mB)v12
多次碰撞后，B停在车右端，系统初动能全部转化为内能，由能量守恒，得FfL＝(mA+mB)v02
联立以上三式，解得
(mA+mB)2＝4(mA－mB)2
即＝，
所以mA＝3mB.
答案：mA＝3mB
11．(4分)在做“验证动量守恒定律”的实验中，小球的落点情况如图6－9所示，入射球A与被碰球B的质量之比为MA∶MB＝3∶2，则实验中碰撞结束时刻两球动量大小之比为pA∶pB＝____________.
图6－9
解析：考查碰撞中动量守恒表达式的应用．实验中碰撞结束时刻的动量之比为＝＝×＝.
答案：1∶2
|
图6－10 |
(1)本实验必须用的测量仪器是____________________________．
(2)需要直接测量的数据是_______________________________．
(3)用测得数据验证动量守恒的关系是______________________．
解析：两球被弹开过程，动量守恒，有mAvA＝mBvB.两球离开水平桌面均做平抛运动，它们在空中的飞行时间相等，故其落地时的水平位移和其弹开后的速度成正比．若以平抛运动时间为时间单位，则平抛初速度在数值上即等于物体的水平位移，故有mAsA＝mBsB.因此，须用天平测出mA、mB，用刻度尺测量sA、sB.
答案：(1)天平、刻度尺
(2)A的质量mA、B的质量mB，A球平抛运动的水平位移sA，B球平抛运动的水平位移sB
(3)mAsA＝mBsB
5．在高速公路上发生一起交通事故，一辆质量为1500 kg向南行驶的长途客车迎面撞上了一质量为3000 kg向北行驶的卡车，碰后两辆车接在一起，并向南滑行了一小段距离后停止．根据测速仪的测定，长途客车碰前以20 m/s的速率行驶，由此可判断卡车碰前的行驶速率( )
A．小于10 m/s
B．大于10 m/s，小于20 m/s
C．大于20 m/s，小于30 m/s
D．大于30 m/s，小于40 m/s
解析：选A.由题意分析可知，客车动量大于卡车动量(碰前)，据此可得出A正确．
|
图6－4 |
A．一定沿v0的方向飞去
B．一定沿v0的反方向飞去
C．不可能做自由落体运动
D．以上说法都不对
解析：选D.根据动量守恒得v′＝.mv可能大于、小于或等于Mv0，所以v′可能小于、大于或等于零．
|
图6－5 |
A．ma>mb B．ma<mb
C．ma＝mb D．无法判断
解析：选B.由图象分析得：整个碰撞过程是运动的，a球去碰撞静止的b球，而碰撞后a球反向运动，b球向前运动，所以b球获得的动量超过原来a球的动量，由动能与动量的数值关系Ek＝，如果是ma>mb，则b球的动能将会大于原来a物体的动能，所以违背了能量守恒，一定是ma<mb，所以A、C、D三个选项错误，B选项正确．
|
图6－6 |
A．整个系统机械能不守恒
B．整个系统动量守恒
C．当木块的速度最大时，小车的速度也最大
D．小车AB向左运动的最大位移等于L
答案：ABC
|
图6－7 |
A．v＝，I＝0 B．v＝，I＝2mv0
C．v＝，I＝ D．v＝，I＝2mv0
解析：选B.本题考查动量守恒定律、冲量．木块和子弹又回到A处时，弹簧恢复原长，弹力对木块和子弹做功为0，故此时木块和子弹的速度仍为子弹刚打入木块时的速度，根据动量守恒定律知v＝，子弹和木块动量变化量为2mv0，由弹簧对其冲量引起，弹簧动量大小未变化，故墙壁对弹簧的冲量也为2mv0，选B.
|
图6－8 |
A．小球可能从圆弧轨道上端抛出而不再回到小车
B．小球可能离开小车水平向左做平抛运动
C．小球可能离开小车做自由落体运动
D．小球可能离开小车水平向右做平抛运动
解析：选BCD.当小球到达光滑轨道最高点处二者具有共同的水平速度，因此不可能从圆弧轨道上端抛出而不回到小车，A错．当小球再次回到小车左端时，由动量、能量守恒知：mv0＝mv1+Mv2，mv02＝mv12+Mv22，
可得v1＝v0，v2＝v0.则当m＝M时，v1＝0，小球离开小车时做自由落体运动，当m＜M，v1＜0，即小球向左做平抛运动离开小车；当m＞M，v1＞0，即小球向右做平抛运动离开小车，B、C、D都对．
1．(2009年丰台区模拟)质量为m的物块以初速度v0从光滑斜面底端向上滑行，到达最高位置后再沿斜面下滑到底端，则物块在此运动过程中( )
A．上滑过程与下滑过程中物块所受重力的冲量相等
B．整个过程中物块所受弹力的冲量为零
C．整个过程中物块的合外力冲量为零
D．整个过程中物块的合外力冲量大小为2mv0
答案：AD
|
图6－1 |
A.a比b先到达S，它们在S点的动量不相等
B．a与b同时到达S，它们在S点的动量不相等
C．a比b先到达S，它们在S点的动量相等
D．b比a先到达S，它们在S点的动量相等
解析：选A.a、b两球到达S点时速度方向不同，故它们的动量不等，C、D错．由机械能守恒定律知，a、b经过同一高度时速率相同，但b在竖直方向的分速度v⊥b始终小于同高度时a球的速度v⊥a，应有平均速度⊥b＜⊥a由t＝知，ta＜tb，所以a先到达S点，A对，B错．
|
图6－2 |
A．Ft，mgt B．Ftcosθ，0
C．mv,0 D．Ft,0
解析：选A.力的冲量等于力和力的作用时间的乘积．
|
图6－3 |
A．半圆槽固定不动时，物体M可滑到半圆槽左边缘B点
B．半圆槽在水平地面上无摩擦滑动时，物体M可滑动到半圆槽左边缘B点
C．半圆槽固定不动时，物体M在滑动过程中机械能守恒
D．半圆槽与水平地面无摩擦时，物体M在滑动过程中机械能守恒
解析：选ABC.对于物体与半圆槽组成的系统，设物体M滑到左边最高点时的共同速度为v，由动量守恒(m+M)v＝0，所以v＝0，由能量守恒可知能滑到B点．
(2008•海南)如图所示，一辆汽车A拉着装有集装箱的拖车B，以速度v1＝30 m/s进入向下倾斜的直车道.车道每100 m下降2 m.为使汽车速度在s＝200 m 的距离内减到v2＝10 m/s，驾驶员必须刹车.假定刹车时地面的摩擦阻力是恒力，且该力的70%作用于拖车B,30%作用于汽车A.已知A的质量m1＝2 000 kg，B的质量m2＝6 000 kg.求汽车与拖车的连接处沿运动方向的相互作用力.(取重力加速度g＝10 m/s2)
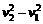＝－2as ①
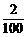＝2×10－2 ③
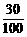F ④
(2009•全国Ⅰ)某同学为了探究物体在斜面上运动时摩擦力与斜面倾角的关系，设计实验装置如图.长直平板一端放在水平桌面上，另一端架在一物块上.在平板上标出A、B两点，B点处放置一光电门，用光电计时器记录滑块通过光电门时挡光的时间.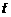
；
；
；
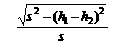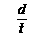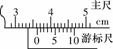③滑块运动时的加速度a＝
；
.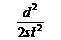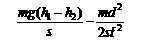