1.圆周运动的动力学问题
[例1]质量为m的物体沿着半径为r的半球形金属球壳滑到最低点时的速度大小为v,如图所示,若物体与球壳之间的动摩擦因数为μ,则物体在最低点时( )
A.向心加速度为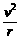 B.向心力为m(g+
B.向心力为m(g+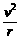 )
)
C.对球壳的压力为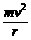 D.受到的摩擦力为μm(g+
D.受到的摩擦力为μm(g+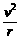 )
)
[解析]物体在最低点沿半径方向受重力、球壳对物体的支持力,两力的合力提供物体做圆周运动在此位置的向心力,由牛顿第二定律有FN-mg=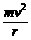 ,物体的向心加速度为
,物体的向心加速度为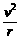 ,向心力为
,向心力为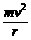 ,物体对球壳的压力为m(g+
,物体对球壳的压力为m(g+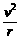 ),在沿速度方向,物体受滑动摩擦力,有F=μFN=μm(g+
),在沿速度方向,物体受滑动摩擦力,有F=μFN=μm(g+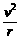 ),综上所述,选项A、D正确.
),综上所述,选项A、D正确.
[答案]AD
[思维提升]匀速圆周运动动力学规律是物体所受合外力提供向心力,即F合=F向,或
F合=m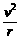 =mω2r=m
=mω2r=m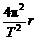 .这一关系是解答匀速圆周运动的关键规律.
.这一关系是解答匀速圆周运动的关键规律.
[拓展1]铁路转弯处的弯道半径r是根据地形决定的,弯道处要求外轨比内轨高,其内外高度差h的设计不仅与r有关,还取决于火车在弯道上行驶的速率.下表中是铁路设计人员技术手册中弯道半径r及与之相对应的轨道的高度差h.
|
弯道半径r(m) |
660 |
330 |
220 |
165 |
132 |
110 |
|
内外轨高度差h(m) |
0.05 |
0.10 |
0.15 |
0.20 |
0.25 |
0.30 |
(1)根据表中数据,试导出h与r关系的表达式,并求出当r=440 m时,h的设计值.
(2)铁路建成后,火车通过弯道时,为保证绝对安全,要求内外轨道均不向车轮施加侧向压力,又已知我国铁路内外轨的距离设计值L=1.435 m,结合表中数据,求出我国火车的转弯速率v.(路轨倾角α很小时,可认为tan α=sin α)
 [解析](1)分析表中数据可得,每组的h与r之乘积均等于常数C=660×50×10-3 m=33 m2,因此h•r=33(或h=
[解析](1)分析表中数据可得,每组的h与r之乘积均等于常数C=660×50×10-3 m=33 m2,因此h•r=33(或h=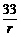 )
)
当r=440 m时,有h=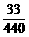 m=0.075
m=75 mm
m=0.075
m=75 mm
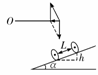
(2)转弯中,当内外轨对车轮均没有侧向压力时,火车的受力如图所示.
由牛顿第二定律得mgtan
α=m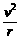 ①
①
因为α很小,有tan
α=sin α=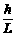 ②
②
由①②可得v=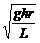
代入数据解得v=15 m/s=54 km/h
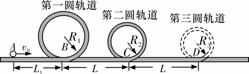 [例2](2009•安徽)过山车是游乐场中常见的设施.下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的三个圆形轨道组成,B、C、D分别是三个圆形轨道的最低点,B、C间距与C、D间距相等,半径R1=2.0
m、R2=1.4
m.一个质量为m=1.0 kg的小球(可视为质点),从轨道的左侧A点以v0=12.0
m/s的初速度沿轨道向右运动,A、B间距L1=6.0
m.小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10 m/s2,计算结果保留小数点后一位数字.试求:
[例2](2009•安徽)过山车是游乐场中常见的设施.下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的三个圆形轨道组成,B、C、D分别是三个圆形轨道的最低点,B、C间距与C、D间距相等,半径R1=2.0
m、R2=1.4
m.一个质量为m=1.0 kg的小球(可视为质点),从轨道的左侧A点以v0=12.0
m/s的初速度沿轨道向右运动,A、B间距L1=6.0
m.小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10 m/s2,计算结果保留小数点后一位数字.试求: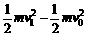 ①
①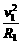 ②
②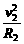 ④
④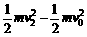 ⑤
⑤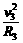 ⑦
⑦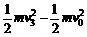 ⑧
⑧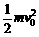
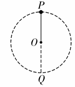 [拓展2]如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是( BC )
[拓展2]如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是( BC )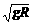 ,此时细绳拉力为零,A错,C对;束缚物是细杆时,如果最高点的速度为
,此时细绳拉力为零,A错,C对;束缚物是细杆时,如果最高点的速度为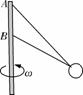 [例3]如图所示,两绳系一质量为m=0.1 kg的小球,两绳的另一端分别固定于轴的A、B两处,上面绳长l=2 m,两绳拉直时与轴的夹角分别为30°和45°,问球的角速度在什么范围内两绳始终有张力(取g=10 m/s2)?
[例3]如图所示,两绳系一质量为m=0.1 kg的小球,两绳的另一端分别固定于轴的A、B两处,上面绳长l=2 m,两绳拉直时与轴的夹角分别为30°和45°,问球的角速度在什么范围内两绳始终有张力(取g=10 m/s2)?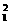 lsin θ ①
lsin θ ①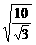 rad/s
rad/s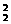 lBsin θ ③
lBsin θ ③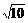 rad/s
rad/s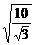 rad/s<ω<
rad/s<ω<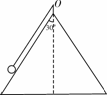 [拓展3]如图所示,一个光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,母线与轴线的夹角θ=30°,一条长为l的绳,一端固定在圆锥体的顶点O,另一端系一个质量为m的小球(可视为质点),小球以速率v绕圆锥体的轴线在水平面内做匀速圆周运动.试分析讨论v从零开始逐渐增大的过程中,球受圆锥面的支持力及摆角的变化情况.
[拓展3]如图所示,一个光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,母线与轴线的夹角θ=30°,一条长为l的绳,一端固定在圆锥体的顶点O,另一端系一个质量为m的小球(可视为质点),小球以速率v绕圆锥体的轴线在水平面内做匀速圆周运动.试分析讨论v从零开始逐渐增大的过程中,球受圆锥面的支持力及摆角的变化情况.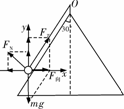 [解析](1)临界条件:小球刚好对锥面没有压力时的速率为v0,小球受重力和绳子的拉力的合力提供向心力,则有F向=mgtan 30° =m
[解析](1)临界条件:小球刚好对锥面没有压力时的速率为v0,小球受重力和绳子的拉力的合力提供向心力,则有F向=mgtan 30° =m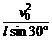 ,解得v0=
,解得v0=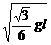
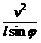
 速度越大,绳与轴线夹角φ越大.
速度越大,绳与轴线夹角φ越大.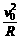 ①
①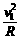 ②
②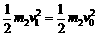 ③
③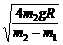
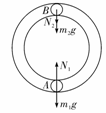 [错因]错解形成的主要原因是向心力的分析中缺乏规范的解题过程.没有作受力分析,导致漏掉重力,表面上分析出了N1=N2,但实际并没有真正明白为什么圆管给m2向下的力.总之从根本上看还是解决力学问题的基本功--受力分析不过关.
[错因]错解形成的主要原因是向心力的分析中缺乏规范的解题过程.没有作受力分析,导致漏掉重力,表面上分析出了N1=N2,但实际并没有真正明白为什么圆管给m2向下的力.总之从根本上看还是解决力学问题的基本功--受力分析不过关.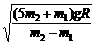
 典例精析
典例精析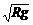 .绳与小球的情况即为此类临界问题,因为绳只能提供拉力不能提供支持力.
.绳与小球的情况即为此类临界问题,因为绳只能提供拉力不能提供支持力.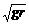 .
.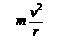 = mω2r =
= mω2r =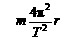 .
.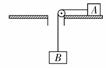 [例3]如图所示,水平转盘的中心有个竖直小圆筒,质量为m的物体A放在转盘上,A到竖直筒中心的距离为r.物体A通过轻绳、无摩擦的滑轮与物体B相连,B与A质量相同.物体A与转盘间的最大静摩擦力是正压力的μ倍,则转盘转动的角速度在什么范围内,物体A才能随盘转动.
[例3]如图所示,水平转盘的中心有个竖直小圆筒,质量为m的物体A放在转盘上,A到竖直筒中心的距离为r.物体A通过轻绳、无摩擦的滑轮与物体B相连,B与A质量相同.物体A与转盘间的最大静摩擦力是正压力的μ倍,则转盘转动的角速度在什么范围内,物体A才能随盘转动.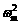 r ①
r ①
 r ①
r ①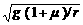
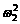 r ④
r ④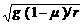 要使A随盘一起转动,其角速度ω应满足
要使A随盘一起转动,其角速度ω应满足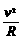 ,代入数据可求得v≤10
m/s
,代入数据可求得v≤10
m/s 易错门诊
易错门诊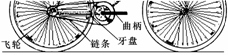 [例1](2009•上海)小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:在时间t内踏脚板转动的圈数为N,那么踏脚板转动的角速度ω= ;要推算自行车的骑行速度,还需要测量的物理量有 ;自行车骑行速度的计算公式v= .
[例1](2009•上海)小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:在时间t内踏脚板转动的圈数为N,那么踏脚板转动的角速度ω= ;要推算自行车的骑行速度,还需要测量的物理量有 ;自行车骑行速度的计算公式v= .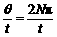 ;要求自行车的骑行速度,还要知道自行车后轮的半径R,牙盘的半径r1、飞轮的半径r2、自行车后轮的半径R;由v1=ωr1=v2=ω2r2,又ω2=ω后,而v=ω后R,以上各式联立解得v=
;要求自行车的骑行速度,还要知道自行车后轮的半径R,牙盘的半径r1、飞轮的半径r2、自行车后轮的半径R;由v1=ωr1=v2=ω2r2,又ω2=ω后,而v=ω后R,以上各式联立解得v=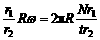
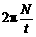 ;牙盘的齿轮数m、飞轮的齿轮数n、自行车后轮的半径R(牙盘的半径r1、飞轮的半径r2、自行车后轮的半径R);
;牙盘的齿轮数m、飞轮的齿轮数n、自行车后轮的半径R(牙盘的半径r1、飞轮的半径r2、自行车后轮的半径R);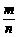 Rω或2πR
Rω或2πR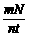 (2πR
(2πR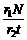 或
或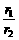 Rω)
Rω)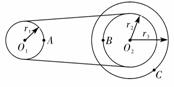 的轴心,轮的半径为r2;r3为与从动轮固定在一起的大轮的半径.已知r2=1.5r1,r3=2r1.A、B、C分别是三个轮边缘上的点,那么质点A、B、C的线速度之比是 3∶3∶4 ,角速度之比是 3∶2∶2 ,向心加速度之比是 9∶6∶8 ,周期之比是 2∶3∶3 .
的轴心,轮的半径为r2;r3为与从动轮固定在一起的大轮的半径.已知r2=1.5r1,r3=2r1.A、B、C分别是三个轮边缘上的点,那么质点A、B、C的线速度之比是 3∶3∶4 ,角速度之比是 3∶2∶2 ,向心加速度之比是 9∶6∶8 ,周期之比是 2∶3∶3 .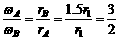
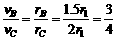
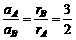
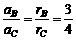
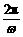 知TA∶TB∶TC=
知TA∶TB∶TC=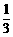 ∶
∶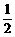 ∶
∶