1.实验:探究弹力与弹簧伸长的关系
[例1]某同学用如图所示装置做探究弹力和弹簧伸长关系的实验.他先测出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上砝码,并逐个增加砝码,测出指针所指的标尺刻度,所得数据列表如下:(重力加速度g取9.8 m/s2)
|
砝码质量 m/102 g |
0 |
1.00 |
2.00 |
3.00 |
4.00 |
5.00 |
6.00 |
7.00 |
|
标尺刻度 x/10-2 m |
15.00 |
18.94 |
22.82 |
26.78 |
30.66 |
34.60 |
42.00 |
54.50 |
(1)根据所测数据,在图坐标纸上作出弹簧指针所指标尺刻度x与砝码质量m的关系曲线.
(2)根据所测得数据和关系曲线可以判断,在 范围内弹力大小与弹簧伸长关系满足胡克定律.这种规格的弹簧劲度系数为 N/m.
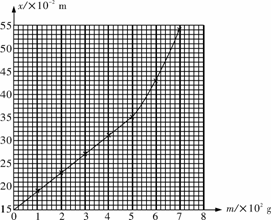 [解析](1)根据表中数据描点,按照各点的分布与走向,作出一条平滑曲线,如图所示.
[解析](1)根据表中数据描点,按照各点的分布与走向,作出一条平滑曲线,如图所示.
(2)由关系曲线可以看出,砝码质量在0-500 g范围内,图线近似为一条直线,即满足弹簧的拉力和形变量成正比(胡克定律).当不挂砝码时,弹簧的长度l0=15×10-2 m.当砝码质量
m=500 g时,l≈35×10-2
m,由ΔF=mg=kΔx解得k=mg/(l-l0)=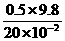 N/m=25 N/m
N/m=25 N/m
[答案](1)见解析 (2)0-500 g;25
[思维提升](1)据所给实验数据描点,然后作出平滑曲线(或直线),注意所画的线不一定过所有点,原则是应尽量使各点较均匀地分布在曲线(或直线)的两侧,描点时要符合客观实际,“曲”、“直”分明.(2)理解坐标的物理含义:x为挂不同砝码时弹簧的长度而不是形变量.(3)曲线的弯曲部分表示弹力超过了弹簧的弹性限度.
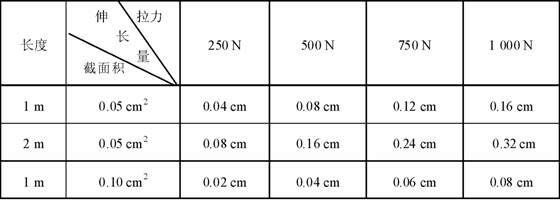 [拓展1]用金属制成的线材(如钢丝、钢筋)受到拉力会伸长,十七世纪英国物理学家胡克发现:金属丝或金属杆在弹性限度内它的伸长与拉力成正比,这就是著名的胡克定律.这一发现为后人对材料的研究奠定了重要基础.现有一根用新材料制成的金属杆,长为4 m,横截面积为0.8 cm2,设计要求它受到拉力后伸长不超过原长的1/1 000,问最大拉力多大?由于这一拉力很大,杆又较长,直接测试有困难,选用同种材料制成样品进行测试,通过测试取得数据如下:
[拓展1]用金属制成的线材(如钢丝、钢筋)受到拉力会伸长,十七世纪英国物理学家胡克发现:金属丝或金属杆在弹性限度内它的伸长与拉力成正比,这就是著名的胡克定律.这一发现为后人对材料的研究奠定了重要基础.现有一根用新材料制成的金属杆,长为4 m,横截面积为0.8 cm2,设计要求它受到拉力后伸长不超过原长的1/1 000,问最大拉力多大?由于这一拉力很大,杆又较长,直接测试有困难,选用同种材料制成样品进行测试,通过测试取得数据如下:
(1)测得结果表明材料受拉力作用后,其伸长量与材料的长度成 正比 ,与材料的截面积成 反比 .
(2)上述金属细杆承受的最大拉力为 104 N.
[解析](1)由题中列表可看出,材料样品的伸长量与材料的长度成正比,与材料的截面积成反比.
(2)由表可看出,材料一定长、一定截面积时,拉力与伸长量的比例为定值.
设1 m长,截面积为0.05 cm 2的比例系数为K1;
2 m长,截面积为0.05 cm2的比例系数为K2;
1 m长,截面积为0.10 cm2的比例系数为K3.
则K1=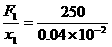 N/m=6.25×105 N/m
N/m=6.25×105 N/m
K2=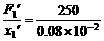 N/m=
N/m= ×6.25×105
N/m
×6.25×105
N/m
K3=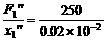 N/m=2×6.25×105 N/m
N/m=2×6.25×105 N/m
由K1、K2、K3的值可得,比例系数K与长度L成反比,与截面积S成正比,故K∝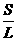
设4 m长,截面积为0.8 cm2的比例系数为K0,
则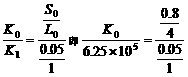
所以K0=2.5×106 N/m
又金属细杆最大伸长量为xm=4×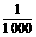 m=4×10-3
m
m=4×10-3
m
所以金属细杆承受的最大拉力为
Fm=K0xm=2.5×106×4×10-3 N=104 N
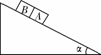 (2008•全国Ⅱ)如图,一固定斜面上两个质量相同的小物块A和B紧挨着匀速下滑,A与B的接触面光滑.已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为α.B与斜面之间的动摩擦因数是( A )
(2008•全国Ⅱ)如图,一固定斜面上两个质量相同的小物块A和B紧挨着匀速下滑,A与B的接触面光滑.已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为α.B与斜面之间的动摩擦因数是( A )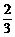 tan α
B.
tan α
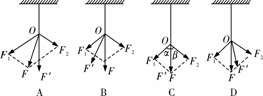
B.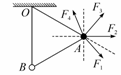 (2007•上海)如图所示,用两根细线把A、B两小球悬挂在天花板上的同一点O,并用第三根细线连接A、B两小球,然后用某个力F作用在小球A上,使三根细线均处于直线状态,且OB细线恰好沿竖直方向,两小球均处于静止状态.则该力可能为图中的( BC )
(2007•上海)如图所示,用两根细线把A、B两小球悬挂在天花板上的同一点O,并用第三根细线连接A、B两小球,然后用某个力F作用在小球A上,使三根细线均处于直线状态,且OB细线恰好沿竖直方向,两小球均处于静止状态.则该力可能为图中的( BC )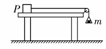 (2007•海南)如图,P是位于水平的粗糙桌面上的物块.用跨过定滑轮的轻绳将P与小盘相连,小盘内有砝码,小盘与砝码的总质量为m.在P运动的过程中,若不计空气阻力,则关于P在水平方向受到的作用力与相应的施力物体,下列说法正确的是( B )
(2007•海南)如图,P是位于水平的粗糙桌面上的物块.用跨过定滑轮的轻绳将P与小盘相连,小盘内有砝码,小盘与砝码的总质量为m.在P运动的过程中,若不计空气阻力,则关于P在水平方向受到的作用力与相应的施力物体,下列说法正确的是( B )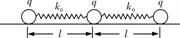 [例1](2009•浙江)如图所示,在光滑绝缘水平面上放置3个电荷量均为q(q>0)的相同小球,小球之间用劲度系数均为k0的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,则每根弹簧的原长为( )
[例1](2009•浙江)如图所示,在光滑绝缘水平面上放置3个电荷量均为q(q>0)的相同小球,小球之间用劲度系数均为k0的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,则每根弹簧的原长为( )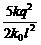 B.l-
B.l-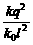 C.l-
C.l-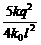 D.l-
D.l-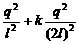 =k0(l-l0),解得l0=l-
=k0(l-l0),解得l0=l-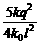
 [例2](2009•北京)如图所示,将质量为m的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则( )
[例2](2009•北京)如图所示,将质量为m的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则( )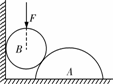 [例3](2008•天津)在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的作用力为F3,若F缓慢增大而整个装置仍保持静止,截面积如图所示,在此过程中( )
[例3](2008•天津)在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的作用力为F3,若F缓慢增大而整个装置仍保持静止,截面积如图所示,在此过程中( )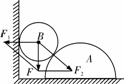 [解析]力F产生了两个作用效果,一个是使B压紧墙面的力F1,一个是压紧A的力F2,当力F缓慢增大时,合力的方向和两个分力的方向都没有发生变化,所以当合力增大时两个分力同时增大.用整体法进行分析,可知地面对A的作用力F3是弹力与摩擦力的合力,摩擦力与F1大小相等,方向相反;弹力与力F和两球重力的合力大小相等,方向相反,C正确.
[解析]力F产生了两个作用效果,一个是使B压紧墙面的力F1,一个是压紧A的力F2,当力F缓慢增大时,合力的方向和两个分力的方向都没有发生变化,所以当合力增大时两个分力同时增大.用整体法进行分析,可知地面对A的作用力F3是弹力与摩擦力的合力,摩擦力与F1大小相等,方向相反;弹力与力F和两球重力的合力大小相等,方向相反,C正确.

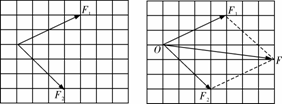
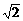
 (1)将三条橡皮条的一端都拴在一个图钉O上,将这三条橡皮条的另一端分别再拴一个图钉A、B、C,注意此时四个图钉均未固定在板上,如图所示.
(1)将三条橡皮条的一端都拴在一个图钉O上,将这三条橡皮条的另一端分别再拴一个图钉A、B、C,注意此时四个图钉均未固定在板上,如图所示. 易错门诊
易错门诊
 典例精析
典例精析