形状相同的图线,在不同的图象中所表示的物理规律不同,通过下图中的例子体会x-t图象和v-t图象中图线表示的物理规律.
|
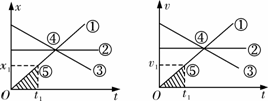
x-t图象 |
v-t图象 |
|
①表示物体做匀速直线运动(斜率表示速度v); ②表示物体静止; ③表示物体向负方向做匀速直线运动; ④交点的纵坐标表示三个运动质点相遇时的位移; ⑤t1时刻物体位移为x1(图中阴影部分的面积没有意义) |
①表示物体做匀加速直线运动(斜率表示加速度a); ②表示物体做匀速直线运动; ③表示物体做匀减速直线运动; ④交点的纵坐标表示三个运动质点的共同速度; ⑤t1时刻物体速度为v1(图中阴影部分面积表示质点①在0-t1时间内的位移) |
 at2=[20×10+
at2=[20×10+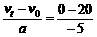 s=4 s
s=4 s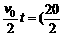 ×4) m=40 m
×4) m=40 m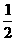 t时的速度为v2,则v1和v2的关系为
( )
t时的速度为v2,则v1和v2的关系为
( )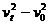 =2a•x
①
=2a•x
① ②
②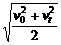 ③
③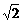 -1)∶(
-1)∶(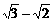 )∶…∶(
)∶…∶(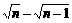 )
)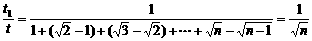
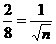 ,n=16,故这列火车共有16节车厢.
,n=16,故这列火车共有16节车厢.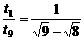 ,t9=
,t9=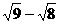 t1=(6-
t1=(6-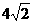 ) s=0.34 s
) s=0.34 s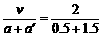 s=1 s
s=1 s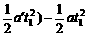 =2×
=2×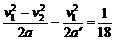 m
m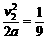 m,所以Δl=l1-l2-l3=
m,所以Δl=l1-l2-l3=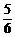 m
m 易错门诊
易错门诊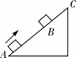 [例1]物体以一定的初速度从A点冲上固定的光滑的斜面,到达斜面最高点C时速度恰好为零,如图所示.已知物体运动到斜面长度3/4处的B点时,所用时间为t,求物体从B运动到C所用的时间.
[例1]物体以一定的初速度从A点冲上固定的光滑的斜面,到达斜面最高点C时速度恰好为零,如图所示.已知物体运动到斜面长度3/4处的B点时,所用时间为t,求物体从B运动到C所用的时间. ,xAC=a(t+tBC)2/2,又xBC=xAC/4
,xAC=a(t+tBC)2/2,又xBC=xAC/4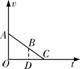 解法三:利用相似三角形面积之比等于对应边平方比的方法,作出v-t图象,如图所示.
解法三:利用相似三角形面积之比等于对应边平方比的方法,作出v-t图象,如图所示.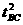 ,解得tBC=t
,解得tBC=t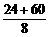 m/s=v0+4a,物体在前4 s内的平均速度等于第2
s末的瞬时速度v2=
m/s=v0+4a,物体在前4 s内的平均速度等于第2
s末的瞬时速度v2=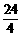 m/s=v0+2a
m/s=v0+2a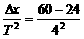 m/s2=2.25 m/s2
m/s2=2.25 m/s2 典例精析
典例精析