0 138018 138026 138032 138036 138042 138044 138048 138054 138056 138062 138068 138072 138074 138078 138084 138086 138092 138096 138098 138102 138104 138108 138110 138112 138113 138114 138116 138117 138118 138120 138122 138126 138128 138132 138134 138138 138144 138146 138152 138156 138158 138162 138168 138174 138176 138182 138186 138188 138194 138198 138204 138212 447348
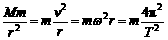 r=ma
r=ma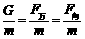 =a向
=a向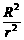 g(R为地球半径,r为轨道半径,g为地球表面的重力加速度)
g(R为地球半径,r为轨道半径,g为地球表面的重力加速度)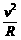
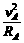 ①
①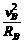 ②
②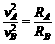 ,所以==2
,所以==2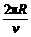 ,所以=·=4×=2
,所以=·=4×=2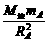 ③
③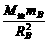 ④
④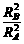 =
=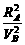 =,所以==
=,所以==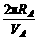 ,TB=
,TB=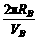 可知=·=·=8∶1
可知=·=·=8∶1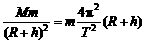
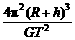 = kg=7.2×1022 kg
= kg=7.2×1022 kg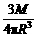 = kg/m3=3.26×103 kg/m3
= kg/m3=3.26×103 kg/m3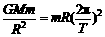 ,再结合ρ=,V=πR3可解得地球的密度ρ=
,再结合ρ=,V=πR3可解得地球的密度ρ=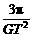 =5.6×103
kg/m3,故行星的密度ρ′=5.32×ρ=2.96×104 kg/m3,D正确.
=5.6×103
kg/m3,故行星的密度ρ′=5.32×ρ=2.96×104 kg/m3,D正确.
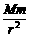 =man=m
=man=m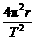 得M=
得M=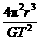 .因此,只需测出卫星(或行星)的运动半径r和周期T,即可算出中心天体的质量M.又由ρ=
.因此,只需测出卫星(或行星)的运动半径r和周期T,即可算出中心天体的质量M.又由ρ=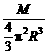 ,可以求出中心天体的密度.
,可以求出中心天体的密度. 典例精析
典例精析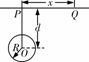 [例1](2009•全国Ⅱ)如图所示,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油.假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向:当存在空腔时,该地区重力加速度的大小和方向会与正常情况下有微小偏离.重力加速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.
[例1](2009•全国Ⅱ)如图所示,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油.假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向:当存在空腔时,该地区重力加速度的大小和方向会与正常情况下有微小偏离.重力加速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.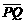 =x,求空腔所引起的Q点处的重力加速度反常;
=x,求空腔所引起的Q点处的重力加速度反常;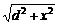 ③
③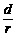 Δg ④
Δg ④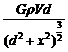 ⑤
⑤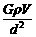 ⑥
⑥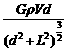 ⑦
⑦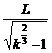 ⑨
⑨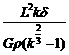 ⑩
⑩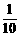 和
和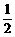 ,地球表面的重力加速度为g,则火星表面的重力加速度约为( B )
,地球表面的重力加速度为g,则火星表面的重力加速度约为( B )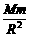 =mg,故火星表面的重力加速度与地球表面的重力加速度的比值
=mg,故火星表面的重力加速度与地球表面的重力加速度的比值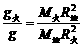 =0.4,故B正确.
=0.4,故B正确.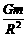
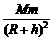 ,g′=
,g′=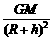
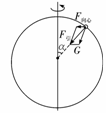 重力:重力是指地球上的物体由于地球的吸引而使物体受到的力.通过分析地球上物体受到地球引力产生的效果,可以知道重力是引力的一个分力.引力的另一个分力是地球上的物体随同地球自转的向心力(这个向心力也可以看做是物体受到的地球引力与地面支持力的合力)如图所示.但由于向心力很小,所以在一般计算中可认为重力近似等于万有引力,重力方向竖直向下(即指向地心).
重力:重力是指地球上的物体由于地球的吸引而使物体受到的力.通过分析地球上物体受到地球引力产生的效果,可以知道重力是引力的一个分力.引力的另一个分力是地球上的物体随同地球自转的向心力(这个向心力也可以看做是物体受到的地球引力与地面支持力的合力)如图所示.但由于向心力很小,所以在一般计算中可认为重力近似等于万有引力,重力方向竖直向下(即指向地心).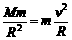 得v=
得v=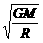 ,所以R越大,v越小;
,所以R越大,v越小; ,所以R越大,ω越小;
,所以R越大,ω越小;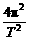 R得T=
R得T=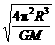 ,所以R越大,T越大;
,所以R越大,T越大;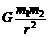 ,其中G=6.67×10-11
N•m2/kg2,叫 引力常量 .
,其中G=6.67×10-11
N•m2/kg2,叫 引力常量 .