15.(12分)2007年10月24日18时,“嫦娥一号”卫星星箭成功分离,卫星进入绕地轨道.在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④.11月5日11时,当卫星经过距月球表面高度为h的A点时,再一次实施变轨,进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦.如图4-12所示.已知月球半径为R.
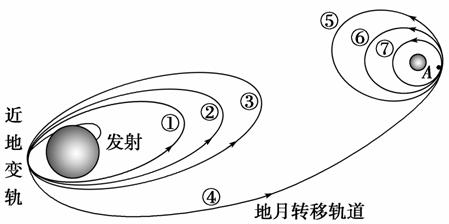
图4-12
(1)请回答:“嫦娥一号”在完成三次近地变轨时需要加速还是减速?
(2)写出月球表面重力加速度的表达式.
解析:(1)加速.
(2)设月球表面的重力加速度为g月,在月球表面有
G=mg月
卫星在极月圆轨道有
=m()2(R+h)
解得g月=.
答案:(1)加速 (2)
|
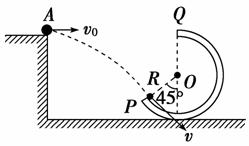 16.(12分)(2010年北京西城区模拟)如图4-13所示,竖直平面内有一光滑圆弧轨道,其半径为R,平台与轨道的最高点等高,一小球从平台边缘的A处水平射出,恰能沿圆弧轨道上的P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为45°,试求:
16.(12分)(2010年北京西城区模拟)如图4-13所示,竖直平面内有一光滑圆弧轨道,其半径为R,平台与轨道的最高点等高,一小球从平台边缘的A处水平射出,恰能沿圆弧轨道上的P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为45°,试求:
(1)小球从平台上的A点射出时的速度v0;
(2)小球从平台上射出点A到圆轨道入射点P之间的距离l;
(3)小球能否沿轨道通过圆弧的最高点?请说明理由.
解析:(1)小球从A到P的高度差
h=R(1+cos45°)=(+1)R,小球做平抛运动,
h=gt2,
小球平抛时间
t= =,
则小球在P点的竖直分速度vy=gt= .
把小球在P点的速度分解可得v0=vy,所以小球平抛初速度v0=
(2)小球平抛下降高度
h=vy·t,
水平射程
s=v0t=2h,
故A、P间的距离
l==h=(+)R.
(3)能.小球从A到达Q时,根据机械能守恒定律可得
vQ=v0=>,所以小球能通过圆弧轨道的最高点.
答案:(1) (2)(+)R (3)能,理由见解析
|
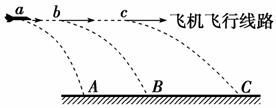 13.(10分)如图4-10所示,在一次执行特殊任务的过程中,在距地面80 m高的水平面上做匀加速直线运动的某波音轻型飞机上依次抛出a、b、c三个物体,抛出的时间间隔为1 s,抛出点a、b与b、c间距分别为45 m和55
m,三个物体分别落在水平地面上的A、B、C三处.(g取10
m/s2)求:
13.(10分)如图4-10所示,在一次执行特殊任务的过程中,在距地面80 m高的水平面上做匀加速直线运动的某波音轻型飞机上依次抛出a、b、c三个物体,抛出的时间间隔为1 s,抛出点a、b与b、c间距分别为45 m和55
m,三个物体分别落在水平地面上的A、B、C三处.(g取10
m/s2)求:
(1)飞机飞行的加速度;
(2)刚抛出b物体时飞机的速度大小;
(3)b、c两物体落地点B、C间的距离.
解析:(1)由Δs=aT2,得:
a=Δs/T2==10 m/s2.
(2)匀变速直线运动中,中间时刻的瞬时速度等于这段时间内的平均速度,则有:
vb==50 m/s.
(3)被抛出的物体在竖直方向做的是自由落体运动,设下落时间为t,由h=gt2得:
t= =4 s
故BC=bc+vct-vbt=bc+(vc-vb)t=bc+aTt=95 m.
答案:(1)10 m/s2 (2)50 m/s (3)95 m
14.(10分)在如图4-11所示的装置中,两个光滑的定滑轮的半径很小,表面粗糙的斜面固定在地面上,斜面的倾角为θ=30°.用一根跨过定滑轮的细绳连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内摆动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动.已知乙物体的质量为m=1 kg,若取重力加速度g=10 m/s2.试求:
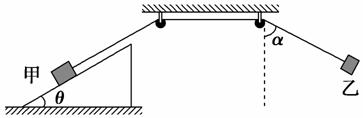
图4-11
(1)乙物体运动经过最高点和最低点时悬绳的拉力大小;
(2)甲物体的质量及斜面对甲物体的最大静摩擦力.
解析:(1)设乙物体运动到最高点时,绳子上的弹力为FT1.
对乙物体FT1=mgcosα=5 N
当乙物体运动到最低点时,绳子上的弹力为FT2
对乙物体由机械能守恒定律:
mgl(1-cosα)=mv2
又由牛顿第二定律:
FT2-mg=m
得:FT2=mg(3-2cosα)=20 N.
(2)设甲物体的质量为M,所受的最大静摩擦力为Ff,乙在最高点时甲物体恰好不下滑,有:Mgsinθ=Ff+FT1
得:Mgsinθ=Ff+mgcosα
乙在最低点时甲物体恰好不上滑,有:
Mgsinθ+Ff=FT2
得:Mgsinθ+Ff=mg(3-2cosα)
可解得:M==2.5 kg
Ff=mg(1-cosα)=7.5 N.
答案:(1)5 N 20 N (2)2.5 kg 7.5 N
|
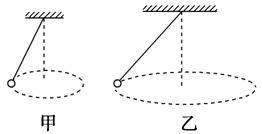 11.用一根细绳,一端系住一定质量的小球,另一端固定,使小球在水平面内做匀速圆周运动.现有两个这样的装置,如图4-8甲和4-8乙所示.已知a,b两小球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两小球的转动半径Ra和Rb之比为________.(sin37°=0.6;cos37°=0.8)
11.用一根细绳,一端系住一定质量的小球,另一端固定,使小球在水平面内做匀速圆周运动.现有两个这样的装置,如图4-8甲和4-8乙所示.已知a,b两小球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两小球的转动半径Ra和Rb之比为________.(sin37°=0.6;cos37°=0.8)
解析:水平面内有:mgtan37°=mω2Ra,mgtan53°=mω2Rb,两式相比可解得:==.
答案:9∶16
12.做杂技表演的汽车从高台水平飞出,在空中运动后着地,一架照相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,并且汽车刚好到达地面时拍到一次.如图4-9所示,已知汽车长度为3.6 m,相邻两次曝光时间间隔相等,由照片(图中实线是用笔画的正方形的格子)可推算出汽车离开高台时的瞬时速度大小为________m/s,高台离地面高度分别为________m.(g取10 m/s2)
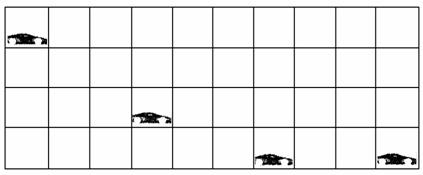
图4-9
解析:从图中可以看出相邻的两次曝光时间间隔内汽车在水平方向上运动的距离为三格,即3.6×3 m=10.8 m.设高台离图中第一次曝光拍照时汽车所在的位置的竖直距离为h,汽车离开高台时的瞬时速度大小为v0,相邻两次曝光时间间隔为t,则竖直方向上利用Δh=gt2得
t= = s=0.6 s
由水平方向的匀速运动可知 www.k@s@5@ 高#考#资#源#网
v0== m/s=18 m/s
从拍摄到的第一张照片和第二张照片得
h=gt02,h+3.6=g(t0+t)2
将t代入解得h=0.45 m,
故高台离地面高度为h+10.8 m=11.25 m.
答案:18 11.25
9.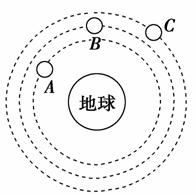 如图4-7所示,在地球同一轨道平面上的三颗不同的人造卫星,关于各物理量的关系,下列说法正确的是( )
如图4-7所示,在地球同一轨道平面上的三颗不同的人造卫星,关于各物理量的关系,下列说法正确的是( )
A.根据v=,可知vA<vB<vC
B.根据万有引力定律,可知FA>FB>FC
C.角速度ωA>ωB>ωC
D.向心加速度aA<aB<aC
|
由G=m有v= ,即卫星的线速度与轨道半径的平方根成反比,A项错.
其向心力就是地球对它的万有引力F=G,因质量关系未知,故B项错.
由G=mrω2有ω= ,即人造卫星的运行角速度与轨道半径三次方的平方根成反比,C项对.
由G=ma有a=,即卫星的向心加速度与轨道半径的平方成反比,故D项错.
7.在高速公路的拐弯处,路面要修建的外高内低,即当车向右拐弯时,司机左侧的路面比右侧的应高一些.路面与水平面的夹角为θ,设拐弯路段是外半径为R的圆弧,要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,θ应等于( )
A.arcsin B.arctan
C.arcsin D.arctan

|
A.(3+)mg B.7mg
C.(2+)mg D.6mg
解析:选A.小球运动到圆轨道水平直径右端时,受绳的拉力F和重力mg,设其速度为v1,到最低点时速度为v2.
由向心力公式=mg
从右端运动到最低点,机械能守恒
mv12+mgr=mv22
FT-mg=m www.k@s@5@ 高#考#资#源#网
FT=3mg+mg=(3+)mg
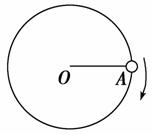
6.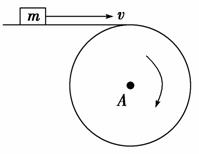 m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图4-5所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑.当m可被水平抛出时,A轮每秒的转数最少是( )
m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图4-5所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑.当m可被水平抛出时,A轮每秒的转数最少是( )
|
C. D.
解析:选A.A轮每秒的转数的最小值对应物体m在A轮正上方时,对传送带的压力恰好为零时A轮的角速度,有:mg=mω2r,又ω=2πn,可得n= ,故A正确.
4.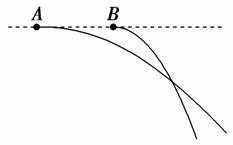 在同一水平直线上的两位置分别沿同方向抛出两小球A和B,其运动轨迹如图4-3所示,不计空气阻力.要使两球在空中相遇,则必须( )
在同一水平直线上的两位置分别沿同方向抛出两小球A和B,其运动轨迹如图4-3所示,不计空气阻力.要使两球在空中相遇,则必须( )
A.先抛出A球
|
C.同时抛出两球
D.A球的初速度大于B球的初速度
解析:选CD.两球在同一水平线上,到相遇点的竖直高度相同,要使两球在空中相遇,两球一定同时抛出,因A球的水平位移大些,因此抛A球的水平速度应大些,故CD正确.
|
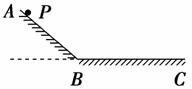 5.(2010年河南省实验中学模拟)如图4-4所示,小球P在A点从静止开始沿光滑的斜面AB运动到B点所用的时间为t1,在A点以一定的初速度水平向右抛出,恰好落在B点所用时间为t2,在A点以较大的初速度水平向右抛出,落在水平面BC上所用时间为t3,则t1、t2和t3的大小关系正确的是( )
5.(2010年河南省实验中学模拟)如图4-4所示,小球P在A点从静止开始沿光滑的斜面AB运动到B点所用的时间为t1,在A点以一定的初速度水平向右抛出,恰好落在B点所用时间为t2,在A点以较大的初速度水平向右抛出,落在水平面BC上所用时间为t3,则t1、t2和t3的大小关系正确的是( )
A.t1>t2=t3 B.t1<t2=t3
C.t1>t2>t3 D.t1<t2<t3
解析:选A.设斜面倾角为θ,A点到BC面的高度为h,则=gsinθt12,平抛落到B点时,h=gt22,以较大的速度平抛,落到BC面上时,h=gt32,可得出:t1= > =t2=t3,故A正确.
3.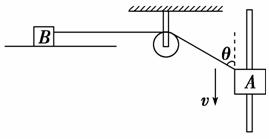 如图4-2所示,沿竖直杆以速度v匀速下滑的物体A通过轻质细绳拉光滑水平面上的物体B,细绳与竖直杆间的夹角为θ,则以下说法正确的是( )
如图4-2所示,沿竖直杆以速度v匀速下滑的物体A通过轻质细绳拉光滑水平面上的物体B,细绳与竖直杆间的夹角为θ,则以下说法正确的是( )
A.物体B向右匀速运动
|
C.细绳对A的拉力逐渐变小
D.细绳对B的拉力逐渐变大
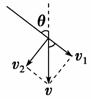 解析:选C.如图沿绳方向的分速度v1=vcosθ.随θ减小v1增大,加速度变小,所以对B的拉力逐渐变小,因此只有C正确.
解析:选C.如图沿绳方向的分速度v1=vcosθ.随θ减小v1增大,加速度变小,所以对B的拉力逐渐变小,因此只有C正确.
1.下列关于运动和力的叙述中,正确的是( )
A.做曲线运动的物体,其加速度方向一定是变化的
B.物体做圆周运动,所受的合力一定指向圆心
C.物体所受合力方向与运动方向相反,该物体一定做直线运动
D.物体运动的速率在增加,所受合力方向一定与运动方向相同
答案:C
|
A.1.8 m/s B.3.2 m/s
C.6.8 m/s D.3.6 m/s www.k@s@5@ 高#考#资#源#网
答案:C