1.探究弹力和弹簧伸长的关系
(1)实验目的
知道弹力与弹簧伸长的定量关系,学会利用列表法、图象法、函数法处理实验数据.
(2)实验原理
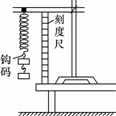
弹簧受力会发生形变,形变的大小与受到的外力有关,沿弹簧的方向拉弹簧,当形变稳定时,弹簧产生的弹力与使它发生形变的拉力在数值上是 相等的 ,用悬挂法测量弹簧的弹力,运用的正是弹簧的弹力与挂在弹簧下面的砝码的重力 相等 .弹簧的长度可用刻度尺直接测出,伸长量可以由 拉长后的长度减去弹簧原来的长度 进行计算.这样可以研究弹簧的弹力和弹簧伸长量之间的定量关系.
 (3)实验器材
(3)实验器材
弹簧、毫米刻度尺、铁架台、钩码若干、 坐标纸 .
(4)实验步骤
①将弹簧的一端挂在铁架台上,让其自然下垂,用刻度尺测出弹簧 自然伸长状态时的长度l0 ,即原长.
②如图所示,将已知质量的钩码挂在弹簧的下端,在平衡时测量 弹簧的总长 并计算 钩码的重力 ,填写在记录表格里.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
F/N |
|
|
|
|
|
|
|
|
L/cm |
|
|
|
|
|
|
|
|
x/cm |
|
|
|
|
|
|
|
③改变所挂钩码的质量,重复前面的实验过程多次.
④以弹力F(大小等于 所挂钩码的重力 )为纵坐标,以 弹簧的伸长量x 为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线.
⑤以 弹簧的伸长量 为自变量,写出曲线所代表的函数.首先尝试一次函数,如果不行则考虑二次函数.
⑥得出弹力和弹簧伸长量之间的定量关系,解释函数表达式中常数的物理意义.
 ①用图钉把白纸钉在水平桌面的方木板上.
①用图钉把白纸钉在水平桌面的方木板上. 用刻度尺作平行四边形,过 O点 画平行四边形的对角线,此对角线即为合力F的图示.
用刻度尺作平行四边形,过 O点 画平行四边形的对角线,此对角线即为合力F的图示.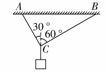 物体平衡中的极值问题
物体平衡中的极值问题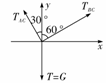 [错解]以重物为研究对象,其受力如图所示.由重物静止有TACcos 30°+TBCcos 60°=G,将TAC=150 N,TBC=100
N代入式解得G=200 N
[错解]以重物为研究对象,其受力如图所示.由重物静止有TACcos 30°+TBCcos 60°=G,将TAC=150 N,TBC=100
N代入式解得G=200 N TBC,当TBC=100
N时,TAC=173.2
N,AC将断.而当TAC=150
N时,TBC=86.6 N<100 N.将TAC=150
N,TBC=86.6
N,代入式②解得G=173.2 N,所以重物的最大重力不能超过173.2 N.
TBC,当TBC=100
N时,TAC=173.2
N,AC将断.而当TAC=150
N时,TBC=86.6 N<100 N.将TAC=150
N,TBC=86.6
N,代入式②解得G=173.2 N,所以重物的最大重力不能超过173.2 N.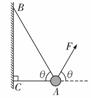 物体平衡中的临界问题分析
物体平衡中的临界问题分析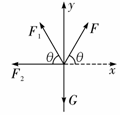 Fsin θ+F1sin θ-mg=0 ①
Fsin θ+F1sin θ-mg=0 ①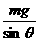 -F1 ③
-F1 ③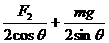 ④
④ 易错门诊
易错门诊 FN2cos(90°-α-β)-FN1sin α=0
FN2cos(90°-α-β)-FN1sin α=0
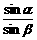 •G
•G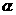 +β)<90°,β↑→cot(
+β)<90°,β↑→cot(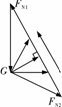
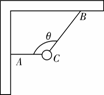 [思维提升]从分析可以看出,解析法严谨,但演算较繁杂,多用于定量分析.图解法直观、鲜明,多用于定性分析.
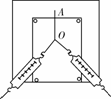
[思维提升]从分析可以看出,解析法严谨,但演算较繁杂,多用于定量分析.图解法直观、鲜明,多用于定性分析.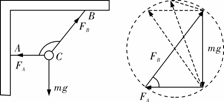 [解析]取球为研究对象,由于球处于一个动态平衡过程,球的受力情况如图所示:重力mg,CA绳的拉力FA,CB绳的拉力FB,这三个力的合力为零,根据平衡条件可以作出mg、FA、FB组成矢量三角形如图所示.将装置顺时针缓慢转动的过程中,mg的大小方向不变,而FA、FB的大小方向均在变,但可注意到FA、FB两力方向的夹角θ不变.那么在矢量三角形中,FA、FB的交点必在以mg所在的边为弦且圆周角为π-θ的圆周上,所以在装置顺时针转动过程中,CA绳的拉力FA大小先增大后减小;CB绳的拉力FB的大小一直在减小.
[解析]取球为研究对象,由于球处于一个动态平衡过程,球的受力情况如图所示:重力mg,CA绳的拉力FA,CB绳的拉力FB,这三个力的合力为零,根据平衡条件可以作出mg、FA、FB组成矢量三角形如图所示.将装置顺时针缓慢转动的过程中,mg的大小方向不变,而FA、FB的大小方向均在变,但可注意到FA、FB两力方向的夹角θ不变.那么在矢量三角形中,FA、FB的交点必在以mg所在的边为弦且圆周角为π-θ的圆周上,所以在装置顺时针转动过程中,CA绳的拉力FA大小先增大后减小;CB绳的拉力FB的大小一直在减小.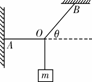 共点力平衡问题的求解方法
共点力平衡问题的求解方法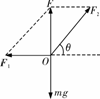 [解析]以结点O为研究对象,受三力而平衡
[解析]以结点O为研究对象,受三力而平衡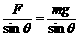
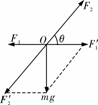 解三角形OF1′(mg)
解三角形OF1′(mg)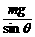
 [拓展1]如图所示,重量为G的均匀链条,两端用等长的轻绳连接,挂在等高的地方,绳与水平线成θ角.试求:
[拓展1]如图所示,重量为G的均匀链条,两端用等长的轻绳连接,挂在等高的地方,绳与水平线成θ角.试求: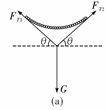 [解析](1)以链条为研究对象时,它受绳子拉力FT1、FT2及重力G的作用,由于链条处于平衡状态,由三力汇交原理知其受力情况如图(a)所示.对整个链条,由正交分解与力的平衡条件得FT1cos
θ=FT2cos
θ
①
[解析](1)以链条为研究对象时,它受绳子拉力FT1、FT2及重力G的作用,由于链条处于平衡状态,由三力汇交原理知其受力情况如图(a)所示.对整个链条,由正交分解与力的平衡条件得FT1cos
θ=FT2cos
θ
① 由①②式得FT1=FT2=
由①②式得FT1=FT2=
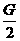 •cot θ(也可以对其竖直方向列式得到FT)
•cot θ(也可以对其竖直方向列式得到FT) 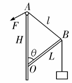 [例2]一轻杆BO,其O端用光滑铰链铰于固定竖直杆AO上,B端挂一重物,且系一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图所示.现将细绳缓慢往左拉,使杆BO与杆AO间的夹角θ逐渐减少,则在此过程中,拉力F及杆BO所受压力FN的大小变化情况是( )
[例2]一轻杆BO,其O端用光滑铰链铰于固定竖直杆AO上,B端挂一重物,且系一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图所示.现将细绳缓慢往左拉,使杆BO与杆AO间的夹角θ逐渐减少,则在此过程中,拉力F及杆BO所受压力FN的大小变化情况是( )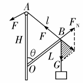 [解析]取BO杆的B端为研究对象,受到绳子拉力(大小为F),BO杆的支持力FN和悬挂重物的绳子的拉力(大小为G)的作用,将FN与G合成,其合力与F等值反向,如图所示,得到一个力三角形(如图中画斜线部分),此力三角形与几何三角形OBA相似.设AO高为H,BO长为L,绳长为l,则由对应边成比例可得
[解析]取BO杆的B端为研究对象,受到绳子拉力(大小为F),BO杆的支持力FN和悬挂重物的绳子的拉力(大小为G)的作用,将FN与G合成,其合力与F等值反向,如图所示,得到一个力三角形(如图中画斜线部分),此力三角形与几何三角形OBA相似.设AO高为H,BO长为L,绳长为l,则由对应边成比例可得 ,式中G、H、L均不变,l逐渐变小,所以可知FN不变,F逐渐变小.故B正确.
,式中G、H、L均不变,l逐渐变小,所以可知FN不变,F逐渐变小.故B正确. [思维提升]利用几何三角形与矢量三角形相似的解题方法是本题创新之处.在运用此法解题时,一般要先构建一个力的矢量三角形,然后再找出一个与之相似的几何三角形,从而得出结果,此法可解决力的复杂变化,如大小和方向都变化的问题.要灵活运用数学知识求解平衡问题.
[思维提升]利用几何三角形与矢量三角形相似的解题方法是本题创新之处.在运用此法解题时,一般要先构建一个力的矢量三角形,然后再找出一个与之相似的几何三角形,从而得出结果,此法可解决力的复杂变化,如大小和方向都变化的问题.要灵活运用数学知识求解平衡问题.