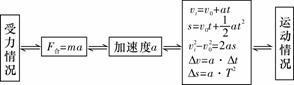
1.临界问题的分析思路
解决临界问题的关键是:认真分析题中的物理情景,将各个过程划分阶段,找出各阶段中物理量发生突变或转折的“临界点”,然后分析出这些“临界点”应符合的临界条件,并将其转化为物理条件.
1.瞬时性问题分析
[例1]如图甲所示,一质量为m的物体系于长度分别为L1、L2的两根细线上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物体处于平衡状态.
(1)现将L2线剪断,求剪断瞬间物体的加速度;
(2)若将图甲中的细线L1改为质量不计的轻弹簧而其余情况不变,如图乙所示,求剪断L2线瞬间物体的加速度.
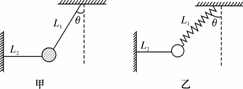
[解析](1)对图甲的情况,L2剪断的瞬间,绳L1不可伸缩,物体的加速度只能沿切线方向,则mgsin θ=ma1
所以a1=gsin θ,方向为垂直L1斜向下.
(2)对图乙的情况,设弹簧上拉力为FT1,L2线上拉力为FT2.重力为mg,物体在三力作用下保持平衡,有
FT1cos θ=mg,FT1sin θ=FT2,FT2=mgtan θ
剪断线的瞬间,FT2突然消失,物体即在FT2反方向获得加速度.因为mgtan θ=ma2,所以加速度a2=gtan θ,方向与FT2反向,即水平向右.
[思维提升](1)力和加速度的瞬时对应性是高考的重点.物体的受力情况应符合物体的运动状态,当外界因素发生变化(如撤力、变力、断绳等)时,需重新进行运动分析和受力分析,切忌想当然;
(2)求解此类瞬时性问题,要注意以下四种理想模型的区别:
|
特性 模型 |
质量 |
内部弹力 |
受外力时 的形变量 |
力能否突变 |
产生拉力或压力 |
|
轻绳 |
不计 |
处处相等 |
微小不计 |
可以突变 |
只有拉力没有压力 |
|
橡皮绳 |
较大 |
一般不能突变 |
只有拉力没有压力 |
||
|
轻弹簧 |
较大 |
一般不能突变 |
既可有拉力 也可有压力 |
||
|
轻杆 |
微小不计 |
可以突变 |
既有拉力也 可有支持力 |
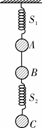 [拓展1]如图所示,弹簧S1的上端固定在天花板上,下端连一小球A,球A与球B之间用线相连.球B与球C之间用弹簧S2相连.A、B、C的质量分别为mA、mB、mC,弹簧与线的质量均不计.开始时它们都处于静止状态.现将A、B间的线突然剪断,求线刚剪断时A、B、C的加速度.
[拓展1]如图所示,弹簧S1的上端固定在天花板上,下端连一小球A,球A与球B之间用线相连.球B与球C之间用弹簧S2相连.A、B、C的质量分别为mA、mB、mC,弹簧与线的质量均不计.开始时它们都处于静止状态.现将A、B间的线突然剪断,求线刚剪断时A、B、C的加速度.
[解析]剪断A、B间的细线前,对A、B、C三球整体分析,弹簧S1中的弹力:
F1=(mA+mB+mC)g ①
方向向上.
对C分析,S2中的弹力:F2=mCg ②
方向向上.
剪断A、B间的细线时,弹簧中的弹力没变.
对A分析:F1-mAg=mAaA ③
对B分析:F2′+mBg=mBaB ④
对C分析:F2-mCg=mCaC ⑤
F2′=F2
由①③式解得aA=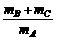 g,方向向上.
g,方向向上.
由②④式解得aB=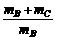 g,方向向下.
g,方向向下.
由②⑤式解得aC=0
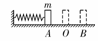 B.物体从A到O速度越来越小,从O到B加速度不变
B.物体从A到O速度越来越小,从O到B加速度不变 越小
越小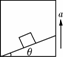 B.当θ一定时,a越大,斜面对物体的摩擦力越大
B.当θ一定时,a越大,斜面对物体的摩擦力越大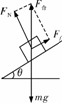 [解析]解法一:用合成法,根据平行四边形定则求解.对物体作受力分析,如图所示.(设物体质量为m,斜面对物体的正压力为FN,斜面对物体的摩擦力为Ff)物体具有向上的加速度a,由牛顿第二定律及力的合成有
[解析]解法一:用合成法,根据平行四边形定则求解.对物体作受力分析,如图所示.(设物体质量为m,斜面对物体的正压力为FN,斜面对物体的摩擦力为Ff)物体具有向上的加速度a,由牛顿第二定律及力的合成有 -mg=ma
-mg=ma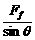 -mg=ma
-mg=ma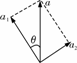 解法二:应用正交分解法求解.
解法二:应用正交分解法求解.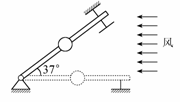 [拓展2]风洞实验中可产生水平方向的、大小可以调节的风力,先将一套有小球的细杆放入风洞实验室,小球孔径略大于细杆直径,如图所示.
[拓展2]风洞实验中可产生水平方向的、大小可以调节的风力,先将一套有小球的细杆放入风洞实验室,小球孔径略大于细杆直径,如图所示.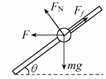 [解析](1)设小球所受的风力为F,支持力为FN、摩擦力为Ff、小球质量为m,作小球受力图,如图所示,当杆水平固定,即θ=0时,由题意得F=μmg
[解析](1)设小球所受的风力为F,支持力为FN、摩擦力为Ff、小球质量为m,作小球受力图,如图所示,当杆水平固定,即θ=0时,由题意得F=μmg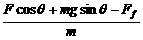 =
=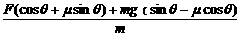
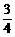 g ④
g ④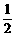 at2 ⑤
at2 ⑤
 易错门诊
易错门诊 典例精析
典例精析