18.(本小题满分12分)
对某种赌博游戏调查后,发现其规则如下:摊主在口袋中装入8枚黑和8枚白的围棋子,参加者从中随意一次摸出5枚,摸一次交手续费1元,而中彩情况如下:
|
摸子情况 |
5枚白 |
4枚白 |
3枚白 |
其它 |
|
彩金 |
20元 |
2元 |
纪念品价值5角 |
无奖同乐一次 |
现在我们试计算如下问题:
(1)求一次获得20元彩金的概率;(结果用最简分数表示)
(2)分别求一次获2元和纪念奖的概率;(结果用最简分数表示)
(3)如果有1000次摸奖,摊主赔钱还是挣钱?是多少元?(精确到元)
解:(1)一次摸奖中20元彩金的概率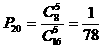 ,可见可能性很小……4分
,可见可能性很小……4分
(2)一次中2元彩金的概率 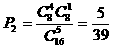 ;……6分
;……6分
而中纪念奖概率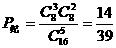 ……8分
……8分
(3)摊主赔钱还是挣钱由其支付完奖金余额决定,1000次收手续费1000元
预计支付20元奖需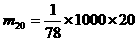 元;
元;
支付2元奖需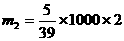 元;
元;
支付纪念奖需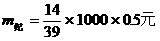
则余额 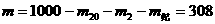 元
元
答:摊主应挣钱308元。 …………12分
(3)另解:摸奖一次得到奖金ξ元,则随机变量ξ的分布列为:
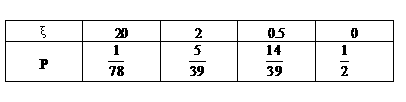
所以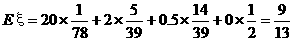 ,
,
所以摊主挣钱,钱数为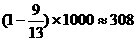 元。
元。
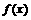 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,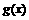 的图象与
的图象与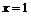 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,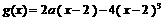 222233.
222233.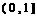 上为增函数,求
上为增函数,求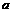 的取值范围;
的取值范围;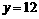 上?若存在,求出
上?若存在,求出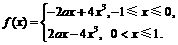 …………………………………………………4分
…………………………………………………4分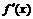 >0对x∈
>0对x∈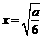 .…………10分 若
.…………10分 若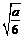 ∈
∈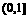 ,即0<a≤6,则
,即0<a≤6,则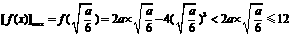 ,
,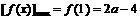 .
.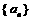 的首项为
的首项为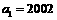 ,公比
,公比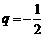 .
.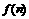 表示该数列的前n项的积,求
表示该数列的前n项的积,求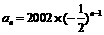 ,
,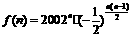 .………………………………4分
.………………………………4分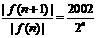 ,
,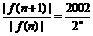 <1,∴ | f(11) |>| f(12) |>….………………8分
<1,∴ | f(11) |>| f(12) |>….………………8分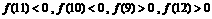 ,∴
,∴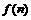 的最大值为
的最大值为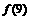 或
或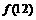 中的最大者.10分
中的最大者.10分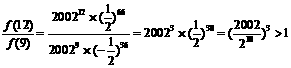 ,
,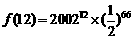 .………………………12分
.………………………12分 是以
是以 为焦点的双曲线C:
为焦点的双曲线C: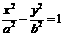 (a>0,b>0)上的一点,已知
(a>0,b>0)上的一点,已知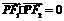 ,
,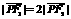 .
.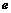 ;
;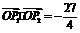 ,
,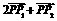 = 0,求双曲线的方程.
= 0,求双曲线的方程.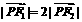 ,
,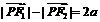 , ∴
, ∴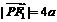 ,
,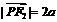 .
. 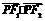 =0,∴(4a)2+(2a)2=(2c)2,∴
=0,∴(4a)2+(2a)2=(2c)2,∴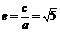 .………………………………4分
.………………………………4分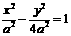 ,渐近线方程为
,渐近线方程为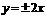 .…5分
.…5分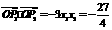 ,∴
,∴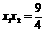 . ∵
. ∵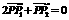 ,∴
,∴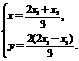 ………8分
………8分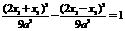 .
.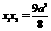 .∴
.∴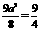 .∴
.∴ 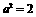 . ∴双曲线的方程为
. ∴双曲线的方程为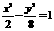 .……12分
.……12分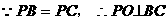
 平面
平面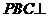 平面ABCD
平面ABCD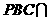 平面ABCD=BC,
平面ABCD=BC,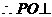 平面ABCD ……2分
平面ABCD ……2分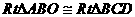
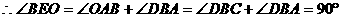 ,即
,即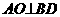
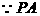 在平面ABCD内的射影为AO,
在平面ABCD内的射影为AO,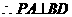 …4分
…4分 ,且平面
,且平面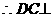 平面PBC
平面PBC 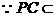 平面PBC,
平面PBC,
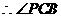 为二面角P-DC-B的平面角 ……6分
为二面角P-DC-B的平面角 ……6分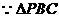 是等边三角形
是等边三角形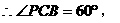 即二面角P-DC-B的大小为
即二面角P-DC-B的大小为 …8分
…8分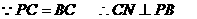 ①
①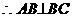 ,且平面
,且平面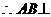 平面PBC ……10分
平面PBC ……10分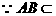 平面PAB
平面PAB  平面
平面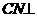 平面PAB…………..10分
平面PAB…………..10分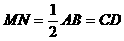 ,得四边形MNCD为平行四边形
,得四边形MNCD为平行四边形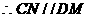
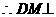 平面PAB
平面PAB 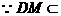 平面PAD
平面PAD 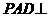 平面PAB ……………….12分
平面PAB ……………….12分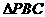 是等边三角形,
是等边三角形, 底面ABCD ……1分
底面ABCD ……1分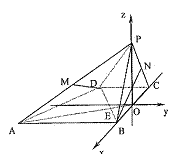
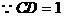 ,则在直角梯形中,
,则在直角梯形中,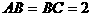
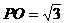 ……3分
……3分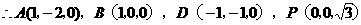
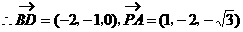 ……4分
……4分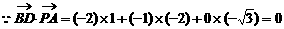
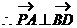 ,即
,即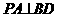 ……6分
……6分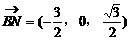
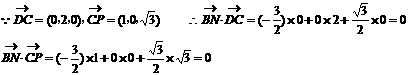
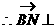 平面PDC,显然
平面PDC,显然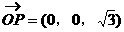 ,且
,且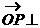 平面ABCD
平面ABCD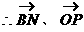 所夹角等于所求二面角的平面角 ……8分
所夹角等于所求二面角的平面角 ……8分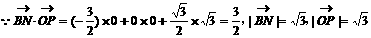
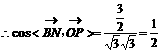
 的大小为
的大小为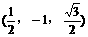
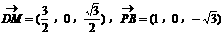 ……12分
……12分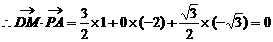
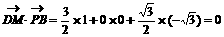
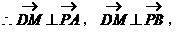 即
即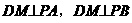
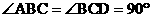 ,AB=BC=PB=PC=2CD=2,侧面
,AB=BC=PB=PC=2CD=2,侧面 底面ABCD,O是BC中点,AO交BD于E.
底面ABCD,O是BC中点,AO交BD于E. ;
; 的大小;
的大小; 平面PAB.、
平面PAB.、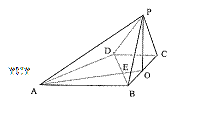
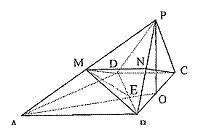
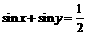 ,
,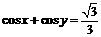 .
.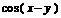 的值; (2)求
的值; (2)求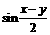 的值.
的值.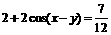 ,故
,故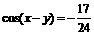 .………7分
.………7分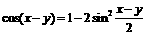 ,∴
,∴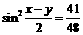 . ∴
. ∴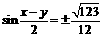 .……12分
.……12分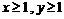 ,且
,且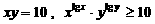 ,则
,则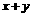 的值是 11 .
的值是 11 .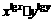 ≥10,得 lg(
≥10,得 lg(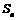 为等差数列
为等差数列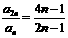 ,则
,则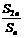 =
.
=
.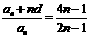 ,得
,得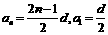 .
.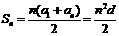 ,
,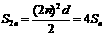 .故
.故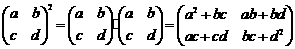 . 则
. 则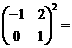 .答
.答 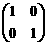 .
.