0 50045 50053 50059 50063 50069 50071 50075 50081 50083 50089 50095 50099 50101 50105 50111 50113 50119 50123 50125 50129 50131 50135 50137 50139 50140 50141 50143 50144 50145 50147 50149 50153 50155 50159 50161 50165 50171 50173 50179 50183 50185 50189 50195 50201 50203 50209 50213 50215 50221 50225 50231 50239 447348
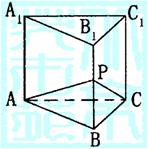 5.如图正三棱柱ABC-A1B1C1底面边长与高相等,截面PAC
5.如图正三棱柱ABC-A1B1C1底面边长与高相等,截面PAC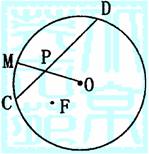 6.如图一圆形纸片的圆心为O,F是圆内一定点,M是圆周
6.如图一圆形纸片的圆心为O,F是圆内一定点,M是圆周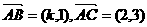 ,则下列k值中能使△ABC是直角三角形的值是 ( )
,则下列k值中能使△ABC是直角三角形的值是 ( )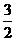 B.
B.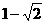 C.
C.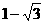 D.-5
D.-5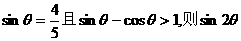 等于 ( )
等于 ( )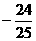 B.
B.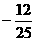 C.
C.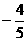 D.
D.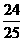
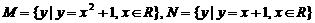 ,那么
,那么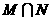 等于( )
等于( )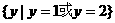 D.
D.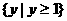
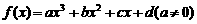 是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.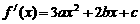
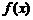 在
在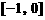 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性, ,得c = 0
,得c = 0 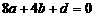 ,即
,即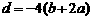
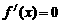 得
得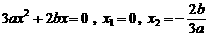
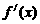 在[0,2]和[4,5]上有相反的
在[0,2]和[4,5]上有相反的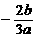 ≤4 Þ -6≤
≤4 Þ -6≤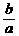 ≤-3
≤-3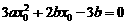

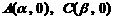 ,依题意可令
,依题意可令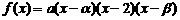
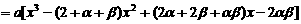
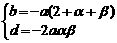 即
即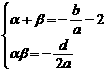
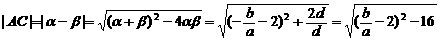
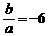 时,
时,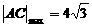 ;
;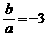 时,
时,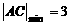 ,故3≤| AC |≤4
,故3≤| AC |≤4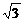
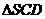 内及其边界上运动,并且总是保持PE
内及其边界上运动,并且总是保持PE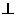 AC.
AC. ,二面角G-CE-D的大小为
,二面角G-CE-D的大小为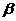 ,求
,求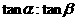 的值.
的值.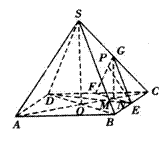 (4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.
(4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.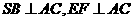 .又
.又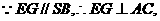
 平面EFG,
平面EFG,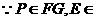 平面EFG,
平面EFG,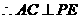 .
.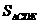 是定值,所以当P到平面CDE的距离最大时,
是定值,所以当P到平面CDE的距离最大时,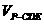 最大,易知当P与G重合时,P到平面CDE的距离最大,故
最大,易知当P与G重合时,P到平面CDE的距离最大,故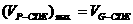 .又
.又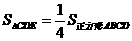 ,G到平面ABCD的距离是点S到平面ABCD的距离的
,G到平面ABCD的距离是点S到平面ABCD的距离的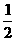 ,
,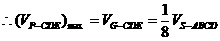 .
.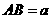 ,EF与AC交于N点,连结GN,则GN
,EF与AC交于N点,连结GN,则GN N是OC的中点,
N是OC的中点, N到BC的距离为
N到BC的距离为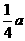 .
.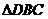 的重心,
的重心,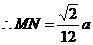 .
.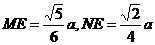 ,
,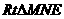 中,容易求得N到DE的距离为
中,容易求得N到DE的距离为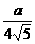 .
.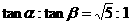 .
.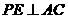 ,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,
,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,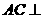 平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E
平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E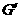 //SB,E
//SB,E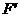 //BD,分别交SC于
//BD,分别交SC于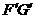 //平面SBD,从而
//平面SBD,从而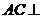 平面E
平面E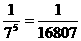 (6`)
(6`)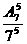 =
=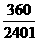 (12`)
(12`)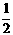 .
.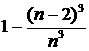 ,
,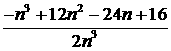 .
.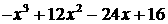 , x>2.
, x>2.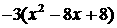 ,
,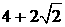 ,
,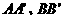 ,则由第二定义得:
,则由第二定义得:
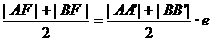
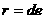
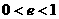 ,此时
,此时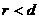 . 相离
. 相离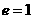 ,此时
,此时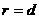 . 相切
. 相切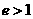 ,此时
,此时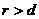 . 相交
. 相交