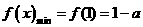19.(本小题13分)
解: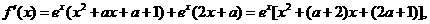
令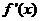 =0得
=0得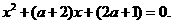
(1)当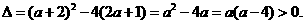
即 <0或
<0或 >4时
>4时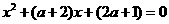 有两个不同的实根
有两个不同的实根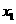 ,
,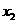 ,不妨设
,不妨设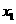 <
<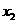
于是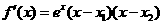 ,从而有下表
,从而有下表
|
x |
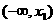 |
x1 |
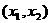 |
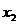 |
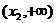 |
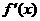 |
+ |
0 |
- |
0 |
+ |
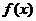 |
↑ |
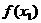 为极大值 为极大值 |
↓ |
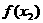 为极小值 为极小值 |
↑ |
即此时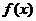 有两个极值点.
有两个极值点.
(2)当△=0即 =0或
=0或 =4时,方程
=4时,方程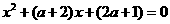 有两个相同的实根
有两个相同的实根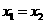
于是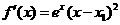
故当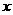 <
<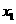 时
时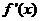 >0,当
>0,当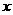 >
>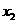 时
时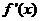 >0,因此
>0,因此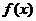 无极值
无极值
(3)当△<0即0< <4时
<4时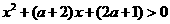
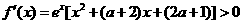 ,故
,故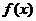 为增函数,此时
为增函数,此时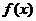 无极值. 因此当
无极值. 因此当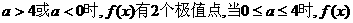 无极值点.
无极值点.
 、
、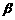 为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )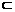
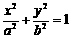 (a > b > 0)上的一点,若
(a > b > 0)上的一点,若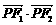 = 0,tan∠PF1F2 =
= 0,tan∠PF1F2 =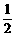 ,则此椭圆的离心率为 ( )
,则此椭圆的离心率为 ( )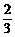 C.
C.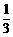 D.
D.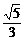
 的图像相邻的两条对称轴之间的距离是
( )
的图像相邻的两条对称轴之间的距离是
( )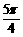 B.5
B.5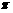 C.
C.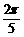 D.
D.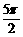
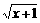 (x < – 1) B.y =
–
(x < – 1) B.y =
–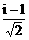 时,z100
+ z50 + 1的值等于
( )
时,z100
+ z50 + 1的值等于
( ) UB)
等于 ( )
UB)
等于 ( ) 函数
函数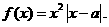
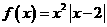 ,则方程f(x)=x即为
,则方程f(x)=x即为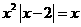
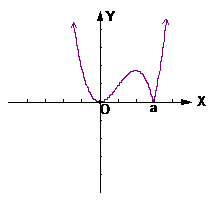
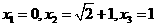

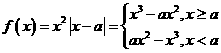 ,
,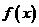 有两个极值点
有两个极值点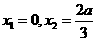 借助于图像可知
借助于图像可知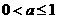 时,函数
时,函数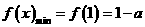
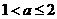 时,显然此时函数的最小值为
时,显然此时函数的最小值为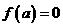
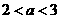 时,
时,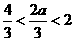 ,此时
,此时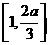 为增函数,在区间
为增函数,在区间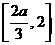 上为减函数,∴
上为减函数,∴ ,又可得
,又可得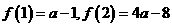
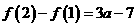
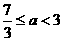 时,
时,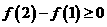 ,此时
,此时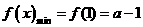
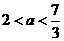 时,
时,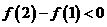 ,此时
,此时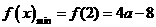
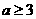 时,
时,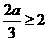 ,此时
,此时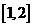 为增函数,故
为增函数,故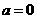 时,
时,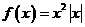 ,此时
,此时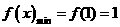
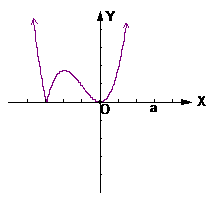
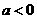 时,其草图见右
时,其草图见右