摘要:22. 设是定义在[-1.1]上的偶函数.的图象与的图象关于直线对称.且当x∈[ 2.3 ] 时. 222233. (1)求的解析式, (2)若在上为增函数.求的取值范围, (3)是否存在正整数.使的图象的最高点落在直线上?若存在.求出的值,若不存在.请说明理由. 解:(1)当x∈[-1.0]时.2-x∈[2.3].f(x)=g(2-x)= -2ax+4x3,当x∈时.f(x)=f(-x)=2ax-4x3. ∴-------------------4分 (2)由题设知.>0对x∈恒成立.即2a-12x2>0对x∈恒成立.于是.a>6x2.从而a>(6x2)max=6.-------------------8分 (3)因f(x)为偶函数.故只需研究函数f(x)=2ax-4x3在x∈的最大值. 令=2a-12x2=0.得.----10分 若∈.即0<a≤6.则 . 故此时不存在符合题意的, 若>1.即a>6.则在上为增函数.于是. 令2a-4=12.故a=8. 综上.存在a = 8满足题设.-----------14分
网址:http://m.1010jiajiao.com/timu3_id_501240[举报]
(本小题满分14分)
设 是定义在
是定义在 上的函数,用分点
上的函数,用分点
将区间 任意划分成
任意划分成 个小区间,如果存在一个常数
个小区间,如果存在一个常数 ,使得和式
,使得和式 (
( )恒成立,则称
)恒成立,则称 为
为 上的有界变差函数.
上的有界变差函数.
(1)函数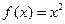 在
在 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;
(2)设函数 是
是 上的单调递减函数,证明:
上的单调递减函数,证明: 为
为 上的有界变差函数;
上的有界变差函数;
(3)若定义在 上的函数
上的函数 满足:存在常数
满足:存在常数 ,使得对于任意的
,使得对于任意的 、
、 时,
时, .证明:
.证明: 为
为 上的有界变差函数.
上的有界变差函数.
(本小题满分14分)
设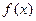 是定义在
是定义在 上的函数,用分点
上的函数,用分点
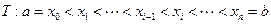
将区间 任意划分成
任意划分成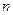 个小区间,如果存在一个常数
个小区间,如果存在一个常数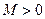 ,使得和式
,使得和式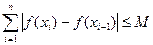 (
(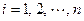 )恒成立,则称
)恒成立,则称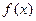 为
为 上的有界变差函数.
上的有界变差函数.
(1)函数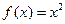 在
在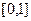 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;
(2)设函数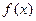 是
是 上的单调递减函数,证明:
上的单调递减函数,证明: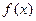 为
为 上的有界变差函数;
上的有界变差函数;
(3)若定义在 上的函数
上的函数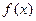 满足:存在常数
满足:存在常数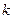 ,使得对于任意的
,使得对于任意的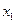 、
、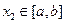 时,
时,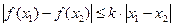 .证明:
.证明: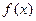 为
为 上的有界变差函数.
上的有界变差函数.
设
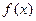 是定义在
是定义在 上的函数,用分点
上的函数,用分点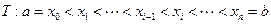
将区间
 任意划分成
任意划分成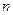 个小区间,如果存在一个常数
个小区间,如果存在一个常数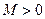 ,使得和式
,使得和式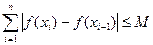 (
(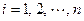 )恒成立,则称
)恒成立,则称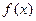 为
为 上的有界变差函数.
上的有界变差函数.(1)函数
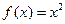 在
在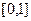 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;(2)设函数
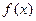 是
是 上的单调递减函数,证明:
上的单调递减函数,证明: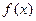 为
为 上的有界变差函数;
上的有界变差函数;(3)若定义在
 上的函数
上的函数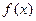 满足:存在常数
满足:存在常数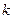 ,使得对于任意的
,使得对于任意的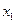 、
、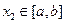 时,
时,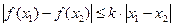 .证明:
.证明: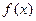 为
为 上的有界变差函数.
上的有界变差函数.(本小题满分14分)
设![]() ,
,![]() 是平面直角坐标系
是平面直角坐标系![]() 上的两点,现定义由点
上的两点,现定义由点![]() 到点
到点![]() 的一种折线距离
的一种折线距离![]() 为
为
![]()
对于平面![]() 上给定的不同的两点
上给定的不同的两点![]() ,
,![]() ,
,
(1)若点![]() 是平面
是平面![]() 上的点,试证明
上的点,试证明![]()
(2)在平面![]() 上是否存在点
上是否存在点![]() ,同时满足
,同时满足
①![]() ②
② ![]()
若存在,请求出所有符合条件的点,请予以证明。
查看习题详情和答案>> ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
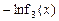 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值; ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.