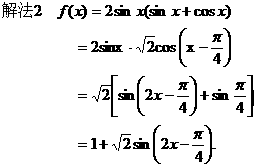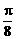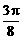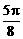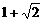20.A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是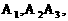 B队队员是
B队队员是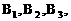 按以往多次比赛的统计,对阵队员之间胜负概率如下:
按以往多次比赛的统计,对阵队员之间胜负概率如下:
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后所得总分分别为ξ、η.
|
对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
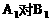 |
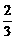 |
 |
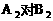 |
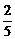 |
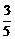 |
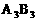 |
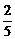 |
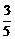 |
(Ⅰ)求ξ,η的概率分布;
(Ⅱ)求Eξ,Eη.
[命题意图] 本题主要考查离散型随机变量分布列和数学期望等概念与计算,以及运用概率知识认识和讨论实际问题的能力.
该题的取材贴近考生日常生活,以广大考生都熟悉的乒乓球比赛为素材,用列表的方式,给出对阵队员间胜负的概率,并规定每场胜负的得分规则.这样的条件下,赛后球队所得总分是离散型随机变量.本题要求考生计算该随机变量的分布列和数学期望.
这样设计试题,应用性强,也能贴近考生实际,符合《考试说明》的要求.
[解题思路] 为了求随机变量ξ和η的概率分布,必须先确定它们是离散型还是连续型.依题意,它们都是离散型随机变量,且满足ξ+η=3.所以只须求出ξ(或η)的概率分布,便可立即写出η(或ξ)的概率分布.
为了求ξ的概率分布,首先应弄清ξ可能取哪些值?这些值表示怎样的随机事件?进而应用随机事件概率计算公式(如乘法公式、加法公式等),求出ξ取每一个可能值的概率,使得到所要求的概率分布列.
至于第(Ⅱ)问,可直接应用离散型随机变量数学期望的计算公式求解.
因为ξ是A队赛后所得的总分,根据题意,ξ只可能取0,1,2,3等4个值,其表示的随机事件分别为:
ξ=表示A队3场比赛都输球,全负;
ξ=1表示A队3场比赛中1胜2负;
ξ=2表示A队3场比赛中2胜1负;
ξ=3表示A队3场比赛全胜.
所以由给出的胜负概率表,应用互斥事件概率的加法公式、独立事件的概率加法公式等相关公式,便可求得ξ的分布列.
(Ⅰ)解 ξ、η的可能取值都为3,2,1,0.ξ的分布为:

依题意,ξ+η=3,故η的分布为:


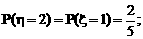

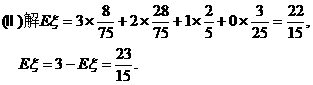
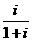 +(1+
+(1+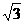 i)2对应的点位于( )
i)2对应的点位于( )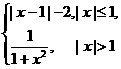 ,则f[f(
,则f[f(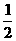 )]=( )
)]=( )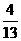 (C)-
(C)-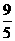 (D)
(D) 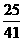
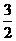 (C)
(C) 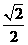 (D)
(D)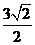
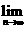
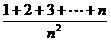 =( )
=( )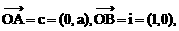 直线
直线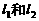 分别过点O和A,其方向向量分别为c+λi和i-2λc,点P是
分别过点O和A,其方向向量分别为c+λi和i-2λc,点P是 的交点.为了求点P的轨迹方程,可采用不同的方法.在这里,有一点值得注意的是:试题本身并没有要求考生求点P的轨迹方程,我们是借助轨迹的思想,只须求出点P的坐标所应满足的方程,进而展开讨论,而无须检验满足方程的每一个解为坐标的点都是符合题意的点P,也即无须要求所得方程的纯粹性,与严格意义上的求轨迹方程有所不同.
的交点.为了求点P的轨迹方程,可采用不同的方法.在这里,有一点值得注意的是:试题本身并没有要求考生求点P的轨迹方程,我们是借助轨迹的思想,只须求出点P的坐标所应满足的方程,进而展开讨论,而无须检验满足方程的每一个解为坐标的点都是符合题意的点P,也即无须要求所得方程的纯粹性,与严格意义上的求轨迹方程有所不同.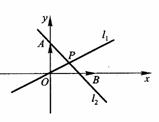
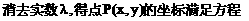

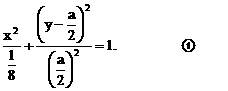
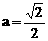 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;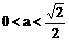 时,方程①表示椭圆,故焦点
时,方程①表示椭圆,故焦点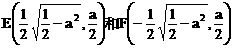 为合乎题意的两个定点;
为合乎题意的两个定点;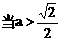 时,方程①也表示椭圆,故焦点
时,方程①也表示椭圆,故焦点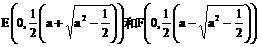 为合乎题意的两个定点.
为合乎题意的两个定点.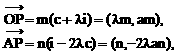
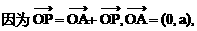
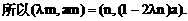
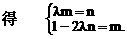
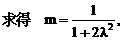
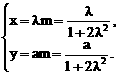
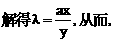
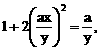
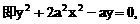
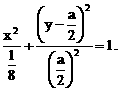
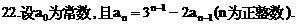
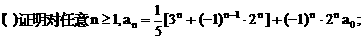
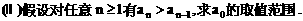
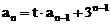 ”.理科试题改变以往给出初始值的做法,给出常数
”.理科试题改变以往给出初始值的做法,给出常数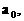 证明数列
证明数列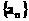 的一个通项公式。这种提问方式反映出新的考查角度,不让考生死套题型,有利于考查独立思考能力和理性思维能力,对文科考生则降低抽象思维的要求,递推关系简化为基本形式“
的一个通项公式。这种提问方式反映出新的考查角度,不让考生死套题型,有利于考查独立思考能力和理性思维能力,对文科考生则降低抽象思维的要求,递推关系简化为基本形式“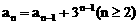 ”,并给出初始值a=1,使试题难度较为切合文科考生的实际.
”,并给出初始值a=1,使试题难度较为切合文科考生的实际.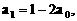 等式成立;
等式成立;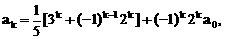
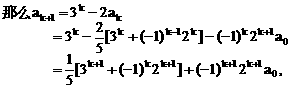
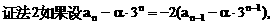
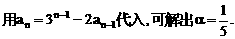
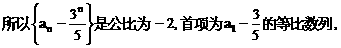
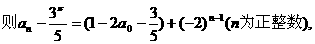
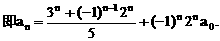
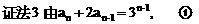
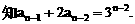
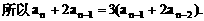
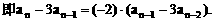
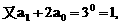
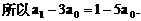
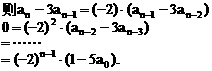
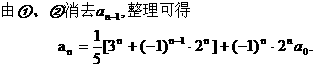
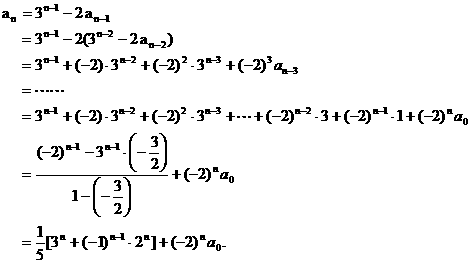
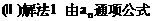
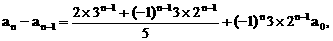
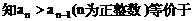
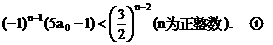
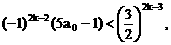
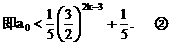
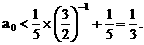
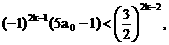
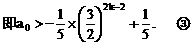

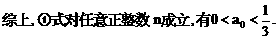

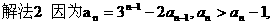
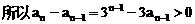


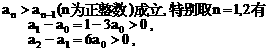

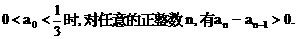
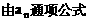

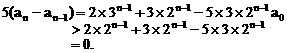
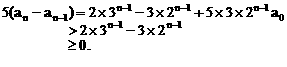

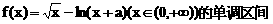 .
. 与对数函数ln(x+a)之差,让考生求这个函数的单调区间.直接应用单调函数的定义,难以进行有效的讨论,宜借助求导的方法求解.以此可以考查函数求导的技能,以及讨论导数正负性的方法.
与对数函数ln(x+a)之差,让考生求这个函数的单调区间.直接应用单调函数的定义,难以进行有效的讨论,宜借助求导的方法求解.以此可以考查函数求导的技能,以及讨论导数正负性的方法.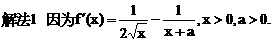
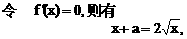

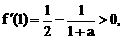
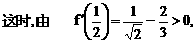

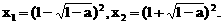
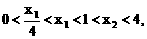
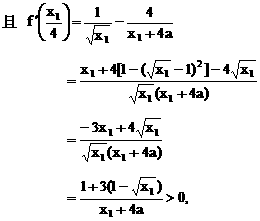
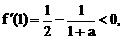

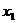 或
或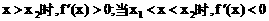
 都是单调区间,f(x)在这两个区间上都是增函数;
都是单调区间,f(x)在这两个区间上都是增函数;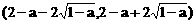 也是单调区间,f(x)在这个区间上是减函数.
也是单调区间,f(x)在这个区间上是减函数.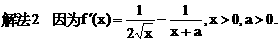
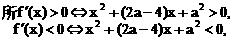
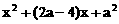
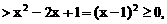
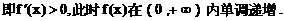
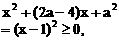
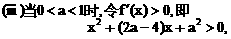
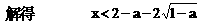
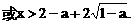
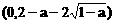 内单调递增,在区间
内单调递增,在区间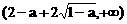 内也单调递增.
内也单调递增.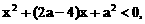
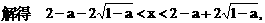
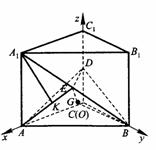
 底面是等腰直角三角形,∠ACB=90°.侧棱
底面是等腰直角三角形,∠ACB=90°.侧棱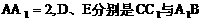 的中点,点E在平面ABD上的射影是△ABD的重心G.
的中点,点E在平面ABD上的射影是△ABD的重心G.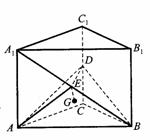
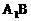 与平面ABD所成角的大小(结果用反三角函数值表示);
与平面ABD所成角的大小(结果用反三角函数值表示);
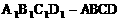 的棱
的棱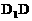 的中点,则正方体的中心O在截面AMC上的射影恰好是△AMC的重心”.试题基本上是采用其逆命题,且只给出半个正方体,把问题提为“正方体的一条对角线与截面所成的角”,隐蔽了上述性质,提高了对考生空间想像力和推理能力的要求,以期更好地考查考生的数学能力.
的中点,则正方体的中心O在截面AMC上的射影恰好是△AMC的重心”.试题基本上是采用其逆命题,且只给出半个正方体,把问题提为“正方体的一条对角线与截面所成的角”,隐蔽了上述性质,提高了对考生空间想像力和推理能力的要求,以期更好地考查考生的数学能力.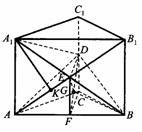
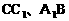 的中点,又DC⊥平面ABC,
的中点,又DC⊥平面ABC,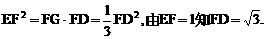
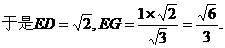
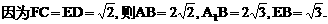
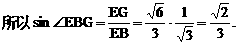

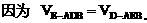
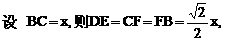
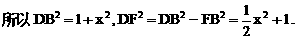

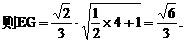
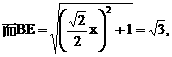
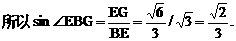

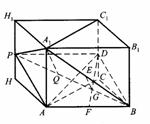
 的中点P,连结PD,PA,PB,则ABDP是平行四边形,PB必过△ADB的重心.
的中点P,连结PD,PA,PB,则ABDP是平行四边形,PB必过△ADB的重心.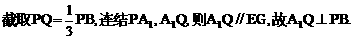
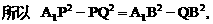
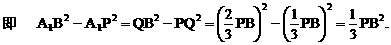

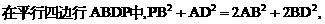
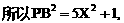
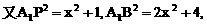
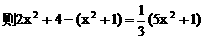
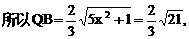
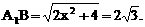


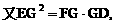
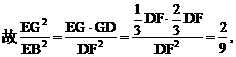
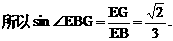
 与平面ABD所成的角.
与平面ABD所成的角.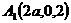 ,E(a,a,1),
,E(a,a,1),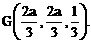
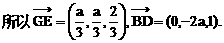
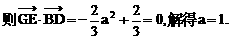
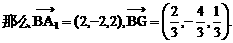
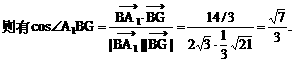
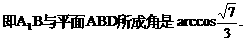


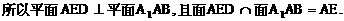
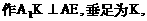
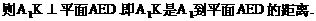
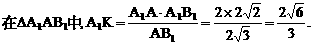
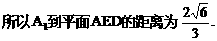

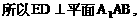
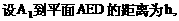
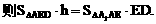
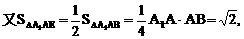
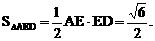
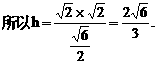

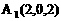 E(1,1,1),D(0,0,1).
E(1,1,1),D(0,0,1).
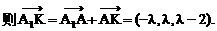
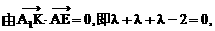


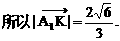

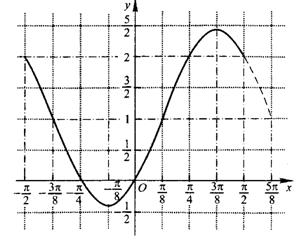
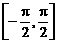 上的图象.
上的图象.