摘要： 如图.点E是正方形ABCD内一点.△CDE是等边三角形.连接EB.EA.延长BE交边AD于点F． (1)求证:△ADE≌△BCE, (2)求∠AFB的度数． [答案]解:(1)∵四边形ABCD是正方形. ∴∠ADC=∠BCD=90°.AD=BC． ∵△CDE是等边三角形. ∴∠CDE=∠DCE=60°.DE=CE． ∵∠ADC=∠BCD=90°.∠CDE=∠DCE=60°. ∴∠ADE=∠BCE=30°． ∵AD=BC.∠ADE=∠BCE.DE=CE. ∴△ADE≌△BCE． (2)∵△ADE≌△BCE. ∴AE=BE. ∴∠BAE=∠ABE． ∵∠BAE+∠DAE=90°.∠ABE+∠AFB=90°.∠BAE=∠ABE. ∴∠DAE=∠AFB． ∵AD=CD=DE. ∴∠DAE=∠DEA． ∵∠ADE=30°. ∴∠DAE=75°. ∴∠AFB=75°．
网址：http://m.1010jiajiao.com/timu3_id_496564[举报]
（2013•泸州模拟）如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF．给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=| 2 |
查看习题详情和答案>>
如图，点E是正方形ABCD边BC的中点，H是BC延长线上的一点，EG⊥AE于点E，交边CD于G，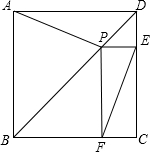
如图，点P是正方形ABCD对角线BD上一点，作PE⊥DC于E，PF⊥BC于F．
（2005•遵义）如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且AE⊥AF，A为垂足．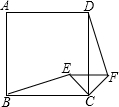
如图，点E是正方形ABCD内一点，把△BEC绕点C旋转至△DFC的位置，则∠EFC的度数是